|
LIGA ZADANIOWA UMK W TORUNIU
ZADANIA W ROKU SZKOLNYM 2006/2007 |
Zadania przygotowawcze do etapu I-go
dla uczniów klas VI szkół podstawowych
|
Tematyka
1. Podzielność liczb.
2. Działania na liczbach wymiernych dodatnich.
3. Podstawowe figury geometryczne i ich pola.
|
| Zadanie 1 |
|
Odkryj zaszyfrowane cyfry w podanym działaniu wiedząc, że te same litery oznaczają te same cyfry, a różnym cyfrom odpowiadają różne litery:
KOT + KOT = TOK.
|
| Zadanie 2 |
Za ile co najmniej lat 10 grudnia wypadnie w sobotę, jak w roku 2005? Podaj co najmniej dwa takie lata jeśli istnieją.
|
| Zadanie 3 |
Oblicz:  . .
|
| Zadanie 4 |
 Oblicz pole prostokąta ABCD na rysunku wiedząc, że liczby wpisane w trzy mniejsze prostokąty są polami tych prostokątów. Oblicz pole prostokąta ABCD na rysunku wiedząc, że liczby wpisane w trzy mniejsze prostokąty są polami tych prostokątów.
|
| Zadanie 5 |
Oblicz: 
|
| Zadanie 6 |
Pewna liczba całkowita przy dzieleniu przez 3 daje resztę 1, zaś przy dzieleniu przez 4 daje resztę 3. Jaką resztę daje ta liczba przy dzieleniu przez 60?
|
| Zadanie 7 |
|
Oblicz: 
.
|
| Zadanie 8 |
Liczba k przy dzieleniu przez 7 daje resztę 4. Liczba t przy dzieleniu przez 7 daje resztę 3. Wyznacz resztę z dzielenia przez 7 iloczynu tych liczb.
|
Rozwiązanie Milosza Paczkowskiego
|
| Zadanie 9 |
Jedenastolitrowe naczynie wypełnione jest mlekiem. Przy pomocy dwóch pustych naczyń o pojemności 3 litry i 5 litrów odmierz dokładnie 4 litry mleka nie tracąc ani kropelki. Pamiętaj, że nie wolno wylewać mleka na zewnątrz.
|
| Zadanie 10 |
Uzasadnij, że każda z liczb 1007, 10017, 100117, ... dzieli się przez 53.
|
Rozwiązanie Bogny Pastwy
|
| Zadanie 11 |
|
Uzasadnij, że równoległoboki ABCD i AEFG mają równe pola. 
|
Rozwiązanie Maćka Perdeni
|
| Zadanie 12 |
Znajdź najmniejszą liczbę czterocyfrową SAAM taką, że MI + FUKO = SAAM.
|
| Zadanie 13 |
Każdy z trzech chłopców ma pewną ilość monet. Pierwszy z nich dał pozostałym tyle monet ile każdy z nich posiadał. Następnie drugi, a potem trzeci z nich postąpił tak samo, tzn. dał dwóm pozostałym tyle monet ile każdy z nich miał aktualnie. W rezultacie okazało się, że na końcu mieli po 8 monet. Ile monet posiadał każdy chłopiec na początku?
|
| Zadanie 14 |
Liczba naturalna nazywa się dobrą jeśli zapisana jest przy pomocy różnych cyfr i iloczyn tych cyfr jest równy 360. Podaj co najmniej dwie takie liczby naturalne. Wyznacz największą liczbę dobrą.
|
Rozwiązanie Jakuba Polaka
|
| Zadanie 15 |
Podaj 2004 cyfrę rozwinięcia dziesiętnego ułamka 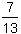 . .
|
| Zadanie 16 |
Jakiego rodzaju jest trójkąt, którego dwa boki mają długości 10 cm i 5 cm, a kat między nimi ma 60°?
|
| Zadanie 17 |
Bak był pełen wody. Wodę z baku przelano do trzech pojemników. To każdego z nich przelano tę samą całkowitą liczbę litrów wody. Okazało się, że w pierwszym pojemniku woda wypełniła 1/2 jego objętości, w drugim 2/3, zaś w trzecim 3/4. Przy jakiej najmniejszej objętości baku jest możliwa taka sytuacja, jeśli objętość baku i pojemników wrażają się liczbami całkowitymi.
|
| Zadanie 18 |
Cenę butów obniżono o 15%, a potem podwyższono o 10% i 2 złote. Obecnie cena butów wynosi 39,4 złotych. Jaka była cena butów przed obniżką, a jaka po obniżce?
|
Rozwiązanie Michaliny Rajczyk
|
| Zadanie 19 |
Liczba naturalna n jest równa sumie pewnych trzech różnych dzielników naturalnych liczby n - 1. Wyznacz wszystkie liczby n o tej własności.
|
Rozwiązanie Bartka Rembezy
|
| Zadanie 20 |
Jak zmienia się iloraz i reszta przy dzieleniu z resztą, jeżeli dzielna i dzielnik zwiększy się trzykrotnie?
|
| Zadanie 21 |
Pewna liczba całkowita przy dzieleniu przez 3 daje resztę 2, zaś przy dzieleniu przez 4 daje resztę 1. Jaką resztę daje ta liczba przy dzieleniu przez 12?
|
| Zadanie 22 |
Dwie liczby zwierciadlane (jedna powstaje z drugiej, gdy ją odczytać od końca na przykład 347 oraz 743 ) pomnożono i otrzymano wynik 92565.Jakie to liczby?
|
| Zadanie 23 |
Dzieląc pewną liczbę naturalną przez 3, 4, 5, 6, 7 otrzymujemy tę samą resztę równą 2.
- Wyznacz najmniejszą liczbę o podanej własności większą niż 10.
- Wyznacz najmniejszą liczbę o podanej własności, która jest ponadto podzielna przez 11.
|
Rozwiązanie Alberta Wolanta
|
| Zadanie 24 |
Średnia arytmetyczna trzech liczb jest równa 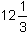 . Jedna z tych liczb jest równa . Jedna z tych liczb jest równa 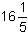 i jest o i jest o 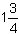 większa od jednej z dwóch pozostałych. Oblicz trzecią liczbę. większa od jednej z dwóch pozostałych. Oblicz trzecią liczbę.
|
| Zadanie 25 |
Znajdź ułamek o mianowniku 250, większy od 0,49 lecz mniejszy od 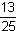 . . |
| Zadanie 26 |
Liczby 1 oraz 5 przedstaw jako sumę skończonej ilości ułamków o licznikach równych 1 i różnych mianownikach.
|
| Zadanie 27 |
|
Nauczyciel rozciął figurę przedstawioną na rys.1 na figury o kształtach przedstawionych na rys.2 i rys.3. Ile figur o kształcie przedstawionym na rys.2 mógł otrzymać przy tym podziale?

|
 .
. Oblicz pole prostokąta ABCD na rysunku wiedząc, że liczby wpisane w trzy mniejsze prostokąty są polami tych prostokątów.
Oblicz pole prostokąta ABCD na rysunku wiedząc, że liczby wpisane w trzy mniejsze prostokąty są polami tych prostokątów.



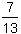 .
. 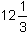 . Jedna z tych liczb jest równa
. Jedna z tych liczb jest równa 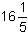 i jest o
i jest o 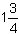 większa od jednej z dwóch pozostałych. Oblicz trzecią liczbę.
większa od jednej z dwóch pozostałych. Oblicz trzecią liczbę. 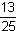 .
.