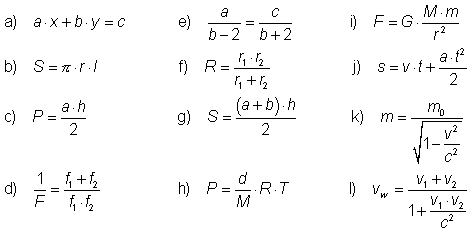Rozmiar: 2560 bajtów Liga Zadaniowa UMK w Toruniu

LIGA ZADANIOWA UMK W TORUNIU

ZADANIA W ROKU SZKOLNYM 2007/2008

Zadania przygotowawcze do etapu III-go dla uczniów klas I gimnazjum
Tematyka:
  1. Równania i nierówności (bez wzorów skróconego mnożenia).
  2. Wielkości wprost i odwrotnie proporcjonalne.
  3. Zadania tekstowe wymagające znajomości rozwiązywania prostych równań i nierówności.
  4. Przekształcanie wzorów.
Zadanie 1
Sześcienny metalowy klocek o krawędzi 10 cm waży 8 kg. Jaką długość ma krawędź klocka sześciennego ważącego 1 kg i wykonanego z tego samego materiału?

Zadanie 2

Na stadionie, którego bieżnia ma 400 m długości odbył się bieg na 10 km. Zwycięzca ukończył bieg po 30 minutach, a ostatni zawodnik po 32 minutach. Po ilu okrążeniach zwycięzca zdublował ostatniego zawodnika? Przyjmij, że każdy zawodnik biegł ze stałą prędkością.

Zadanie 3
Z podanego wzoru wyznacz c.

Następnie oblicz na podstawie otrzymanego wzoru wartość wyrażenia, jeśli x = 1,2 oraz t = 6, zaś y = 3½.

Zadanie 4
Wilgotność skoszonej trawy wynosi 60%, a wilgotność siana równa się 15%. Ile siana otrzyma się z jednej tony trawy?

Zadanie 5

Siedmiu nauczycieli sprawdza 7 kartkówek w ciągu 7 minut. Ile trzeba nauczycieli, aby sprawdzić 77 takich kartkówek w ciągu 77 minut.

Zadanie 6
Cena biletu na mecz piłki nożnej wynosiła 15 zł. Gdy ceną obniżono okazało się, że na mecz przychodzi o 50% widzów więcej, a dochód ze sprzedaży wzrósł o 25%. O ile obniżono ceną biletu?

Zadanie 7
Piętnaście koni w ciągu 50 dni zjada 20 kwintali owsa. Ile kwintali owsa zje 35 koni w ciągu 24 godzin?

Zadanie 8

Średni wiek zawodniczek sekcji gimnastycznej wynosi 11 lat. Najstarsza zawodniczka ma 17 lat, średni wiek pozostałych (bez najstarszej) jest równy 10 lat. Ile zawodniczek jest w sekcji gimnastycznej?

Zadanie 9
Zmniejszając pewną liczbę naturalną o 1, zmniejszamy ją o więcej niż 16,5%. Powiększając zaś tę liczbę o 2, powiększamy ją o mniej niż 33,5%. Wyznacz tę liczbę.

Zadanie 10

W stadzie jest 8 owiec. Pierwsza owca zjada stóg siana w ciągu jednego dnia, druga w ciągu dwóch dni, trzecia w ciągu trzech dni, i tak dalej, ósma w ciągu ośmiu dni. Kto szybciej zje stóg siana: dwie pierwsze owce razem, czy wszystkie pozostałe owce razem?

Zadanie 11
Teofil i młodsza od niego Agata mają razem 105 lat. Różnica ich wieku równa się liczbie lat Agaty wtedy, gdy Teofil miał tyle lat, ile teraz ma Agata.

Zadanie 12

Maharadża obdarował trzy córki perłami przechowywanymi w szkatule. Najstarszej dał połowę zawartości szkatułki j jedną perłę. Drugiej córce dał połowę reszty i jedną perłę, a najmłodszej połowę pozostałych pereł i jeszcze trzy perły, i wówczas szkatułka pozostała pusta. Ile pereł miał Maharadża w szkatule?

Zadanie 13
Mianownik ułamka jest o 2004 większy od licznika. Ułamek ten skrócono i otrzymano 5/17. Znajdź postać tego ułamka przed skróceniem.

Zadanie 14
W jakim wielokącie foremnym kąt wewnętrzny jest równy: (a) 140°, (b) 144°, (c) 150° ?

Zadanie 15
Chemik ma kwas o stężeniu 40% i wodę. Ile powinien wziąć kwasu, a ile wody, by uzyskać 1 litr roztworu o stężeniu 10% ?

Zadanie 16
Podaj miarę kąta wewnętrznego:
  1. sześciokąta foremnego,
  2. ośmiokąta foremnego,
  3. osiemnastokąta foremnego,
  4. stukąta foremnego.

Zadanie 17
Zbyszek mówi do Piotra: "Mam 3 razy więcej lat niż ty miałeś wtedy, kiedy ja miałem tyle lat, ile ty masz teraz. Kiedy osiągniesz mój wiek będziemy mieli łącznie 112 lat."
Ile lat ma Piotr?

Zadanie 18
    Wśród wszystkich prostokątów o obwodzie 100 cm wyznacz ten, który ma największe pole. Odpowiedź uzasadnij.

Zadanie 19
  1. Ile soli należy wsypać do 12 kg wody, aby otrzymać czteroprocentową solankę?
  2. Ile wody należy dodać do 6 kg pięcioprocentowej solanki, aby otrzymać solankę dwuprocentową?
  3. Ile soli należy dosypać do 10 kg pięcioprocentowej solanki, aby otrzymać roztwór dwudziestoprocentowy?
Zadanie 20
Pies goni zająca, który znajduje się w odległości 60 swoich skoków od psa. Gdy zając robi 9 skoków, w tym czasie pies robi 6 skoków. Wielkość 3 psich skoków jest równa 7 skoków zająca. Ile skoków musi zrobić pies, aby dogonić zająca?

Zadanie 21
"4 lata temu byłem 4 razy młodszy od mamy, a 10 lat temu byłem od niej młodszy 10 razy." Ile lat ma autor tej wypowiedzi?

Zadanie 22
Jedna liczba jest większa od drugiej o 406. Jeżeli podzielimy większą liczbę przez mniejszą, to otrzymamy 6 i resztę 66. Wyznacz te liczby.

Zadanie 23
"Która jest teraz godzina" - pyta Michał ojca.
"A policz: do końca doby pozostało 3 razy mniej czasu niż upłynęło od jej początku."
Która jest teraz godzina?

Zadanie 24
Pewną działkę Piotr przekopie w ciągu 12 godzin, Zbyszek w ciągu 10 godzin, a Michał w ciągu 8 godzin. W jakim czasie przekopią tę działkę pracując razem?

Zadanie 25
Statystycznie półtora kota zjada półtorej myszy w ciągu półtora dnia. Ile myszy zje siedem kotów w ciągu tygodnia?

Zadanie 25
Dla jakich wartości m, z odcinków długości 2m + 2, m + 8, 3m + 1 można zbudować trójkąt równoramienny?

Zadanie 26
Z podanych wzorów wyznacz kolejne zmienne: