LIGA ZADANIOWA UMK W TORUNIU
ZADANIA W ROKU SZKOLNYM 2000/2001
Prezent wakacyjny
Zadanie 1
Znaleźć 1000 liczb naturalnych, których suma jest równa iloczynowi.
1) Równanie ilustrujące warunki zadania
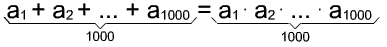
2) Kolejność wyrazów:
a1 Ł a2 Ł ... Ł a1000
3)
a1 . a2 . ... . a1000 Ł 1000 . a1000 /:1000
4) a1 . a2 . ... . a999 Ł 1000
Liczb większych lub równych 2 może być co najwyżej 9, bo 29<1000, a już 210>1000
Zatem jedynek wśród szukanych liczb jest co najmniej 990.
a1 + a2 + ... +a1000 = a1 . a2 . ... .a1000
990 + a991 + a992 + ... +a1000 = a991 . a992 . ... .a1000
Ile maksymalnie może być jedynek?
- Jeśli byłoby 1000 jedynek to otrzymalibyśmy, że 1 + 1 + ... + 1= 1 . 1 . ...1 czyli, że 1000=1, a to nieprawda.
- Jeśli byłoby 999 jedynek to otrzymalibyśmy, że 1 + 1 + ... + 1 + a = 1 . 1 . ...1 .a
to znaczy 999 + a = a czyli 999 = 0, a to też nieprawda.
- Jeśli byłoby 998 jedynek to otrzymalibyśmy, że
1 + 1 + ... + 1 + a999 + a1000 = 1 . 1 . ...1 . a999 . a1000.
Oznaczmy x = a999 y = a1000. Zgodnie z założeniem na początku x Ł y
998 + x + y = x . y
x . y = 998 + x + y | -x -y
xy - x -y = 998
x (y - 1) - y = 998 | + 1
x (y - 1) - y + 1= 999
x (y - 1) - 1 (y - 1) = 999
(y - 1) (x - 1) = 999
(x - 1) (y - 1) = 999
Zadanie sprowadza się więc do przedstawienia liczby 999 w postaci iloczynu dwóch liczb naturalnych.
| 1 . 999 |
|
x = 2 |
|
y = 1000 |
| 3 . 333 |
|
x = 4 |
|
y = 334 |
| 9 . 111 |
|
x = 10 |
|
y = 112 |
| 27 . 37 |
|
x = 28 |
|
y = 38 |
W ten sposób znalazłem 4 rozwiązania, w których tylko dwie liczby nie są jedynkami:
- 1.1.....1.2.1000 = 1+1+...+1+2+1000
- 1.1.....1.4.334 = 1+1+...+1+4+334
- 1.1.....1.10.112 = 1+1+...+1+10+112
- 1.1.....1.28.38 = 1+1+...+1+28+38
Nie jestem przekonany, że są to wszystkie rozwiązania zadania, ale innych nie udało mi się znaleźć. Nie wiem na przykład czy jest takie rozwiązanie gdy 3 liczby nie są jedynkami. Jeśli masz inne rozwiązania, to
napisz do mnie .
Mariusz Banach
![]()