LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA KONKURSOWE Z ETAPU I
DLA KLAS II GIMNAZJUM

Zadanie 3

Ustaw w porządku rosnącym liczby: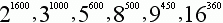

Rozwiązanie

• Zamiast porównywać tak duże wykładniki każdej z potęg zmniejsze 10-krotnie:

  

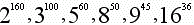
• Następnie korzystam z prawa które mówi "potęgując potęgę mnożymy wykładniki" w celu lepszej możliwości porównania liczb.
  Mam tu 3 liczby które można tak zamienić.

  9⁴⁵ = (3²)⁴⁵ = 3⁹⁰

  16³⁶ = (2⁴)³⁶ = 2¹⁴⁴

  8⁵⁰ = (2³)⁵⁰ = 2¹⁵⁰

• Następnie porównuje liczby o podobnej podstawie i "dobrze skracalnym" wykładniku: 3⁹⁰ i 2¹⁵⁰.
  Dzielę ich wykładniki przez 30 i otrzymuje 3³ i 2⁵
  2⁵ jest większe od 3³, więc 3⁹⁰ jest mniejsze od 2¹⁵⁰
  a co za tym idzie od 2¹⁶⁰.
  
  
• Następnie sprawdzę, która z liczb 3¹⁰⁰ czy 2¹⁵⁰ jest większa.
  Dzielę ich wykładniki przez 50 i wychodzą mi liczby 3² i 2³.
  Liczba 2³ jest mniejsza więc liczba 2¹⁵⁰ jest mniejsza od liczby 3¹⁰⁰.
  
  
• Teraz porównuję potęgę 3⁹⁰ z potęgą 2¹⁴⁴.
  Dielą wykładniki przez 18:
  3⁵ jest mniejsza niż 2⁸ Liczba 3⁹⁰ jest więc mniejsza niż 2¹⁴⁴.
  
  
• Porównajmy liczby 3¹⁰⁰ i 2¹⁶⁰. Podzielmy ich wykładniki przez 20.
  Otrzymujemy liczby 3⁵ i 2⁸.
  Liczba 2⁸ jest większa.

• Muszę sprawdzić teraz ostatnią liczbę czyli 5⁶⁰.
  Liczba 5¹ jest większa do 2²

  Chce porównać ją do najmniejszej liczby ponieważ sadzę że liczba5⁶⁰jest namjniejsza w rzędzie:
  5⁶⁰porównuje do (2²)⁷².
  Liczba 2²)⁷² jest większa, więc liczbą najmniejszą w rzędzie jest 5⁶⁰
  
  Podsumując w porządku rosnącym te liczby wygladają tak: 5⁶⁰,  3⁹⁰, 2¹⁴⁴, 2¹⁵⁰, 3¹⁰⁰, 2¹⁶⁰

Odpowiedz:

5⁶⁰⁰,  9⁴⁵⁰, 16³⁶⁰, 8⁵⁰⁰, 3¹⁰⁰⁰, 2¹⁶⁰⁰.

Jan Rosa IIag.