LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM
zadanie 11
W okrąg wpisano trójkąt ABC, w którym kąt CAB=55 stopni
i ABC=70 stopni. Przez punkt C poprowadzono styczną do okręgu. Styczna ta
przecina przedłużenie boku AB w punkcie D.Oblicz miarę kąta ADC.
Rozwiązanie:
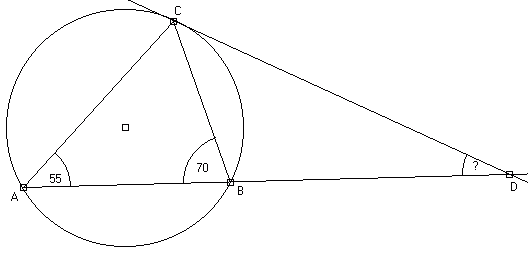
- .Obliczam miarę kąta ACB, czyli ACB = 180-(55+70)=55 stopni.
- .Łączę wierzchołki trójkąta ABC za środkiem okręgu O.
- .Obliczam kąt środkowy AOB oparty na łuku AB. Na tym samym łuku
oparty jest kąt wpisany ACB, więc AOB=55*2=110 stopni.
- .Trójkąt AOB jest równoramienny, o ramionach równych promieniowi okręgu.
Jego kąty wynoszą: 110 , 35 i 35 stopni, bo(180-110):2=35.
Kąt OBD wynosi: 180-35=145 stopni.
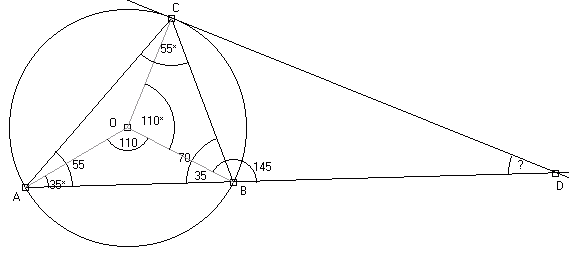
- .Znamy już trzy kąty w czworokącie COBD:
-kąt DCO wynosi 90, bo w punkcie C styczna jest prostopadła do promienia,
-kąt COB ma 110 stopni, ponieważ jest to kąt środkowy, oparty na łuku BC, a kąt wpisany
na tym samym łuku jest dwa razy mniejszy i wynosi 55 stopni.
- .Obliczam kąt ADC, czyli 360-(90+110+145)=360-345=15 stopni.
odpowiedź:
Miara kąta ADC wynosi 15 stopni.
Marcin Korman

