ZADANIA KONKURSOWE Z ETAPU III
DLA KLAS II GIMNAZJUM
Zadanie 2
W okrąg wpisano trójkąt ABC, w którym kąty CAB=30° i ABC=80°. Przez punkt C poprowadzono styczną do okręgu.
Styczna ta przecina przedłużenie boku AB w punkcie D. Oblicz miarę kąta ADC.
Rozwiązanie zadania:
Rozwiązanie zadania przedstawie na dwa sposoby:
I. Za pomocą liczb
II. Za pomocą niewiadomych
I. Wszystko co po kolei zaznaczałam na rysunku opisze w poniższych punktach:
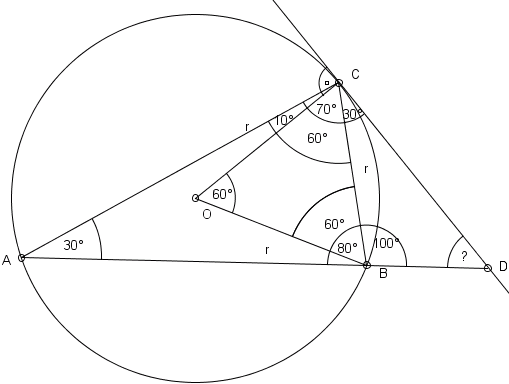
1) O - oznaczyłam środek koła opisanego na trójkącie ABC
2) Kiedy kąt CAB=30°, to kąt środkowy oparty na tym samym łuku ma 60°, co oznacza, że
trójkąt BCO jest równoboczny, czyli zarazem jego wszystkie boki są promieniami okręgu - r
3) Kąt OCD ma 90°, a kąt OCB ma 60°, więc kąt BCD musi mieć 90°-60°=30°
4) Kąt ACB ma 70°, bo 180°-30°-80°=70°, a kąt BCO ma 60°, więc kąt OCA=ACB-OCB=70°-60°=10°
5) Kąt ACD jest sumą kątów: ACO,OCB,BCD, więc 10°+60°+30°=100°
6) Suma kątów w trójkącie wynosi 180°, więc kąt ADC=180°-ACD-DAC=180°-100°-30°=50°
II. Wszystko co po kolei zaznaczałam na rysunku opisze w poniższych punktach:
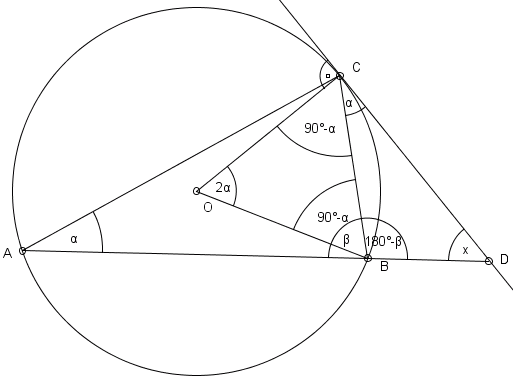
1) O - oznaczyłam środek koła opisanego na trójkącie ABC, kąty CAB oznaczyłam 
i ABC oznaczyłam
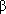, a kąt szukany - x
2) Kat COB jest kątem wpisanym kąta CAB, więc będzie równał się 2
3) Katy OCB i OBC będą równały się po (180°-2
)/2=90°-
4) Kąt OCD=90°, wiec kąt BCD musi równać się
skoro kąt OCB=90°-
5) Kąt przyległy do kąta 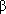, czyli kąt CBD równa się 180°-
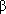
6) Już można obliczyć kąt x na podstawie sumy kątów w trójkącie:
x = 180°-(180°- )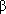
-
x = 180°-180°+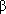
-
x = -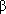
7) Wiemy, że 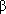= 80° i = 30°, więc wystarczy podstawić liczby i jest odpowiedź na pytanie postawione w poleceniu
Odp. Kąt ADC wynosi 50°.
Stronę opracowała Katarzyna Błażejewska, uczennica klasy II "a"
Gimnazjum nr 11