LIGA ZADANIOWA UMK W TORUNIU 2008/2009
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM

Oblicz pole i obwód zakreskowaniej figury (patrz rysunek obok, na którym dane są długości jego boków oraz jednej z wysokości).

Rozwiązanie:

Najpierw należy zauważyć, że wysokość figury wynosi 1/2 jego boku. Rysujemy odbicie lustrzane trójkąta AFD (aby obliczyć kąt przy wierzchołku A). Powstaje nam trójkąt AED, którego boki mają takie same długości-8 (trójkąt równoboczny). Czyli kąt DAE ma 60^o. Interesująca nas miara kąta DAF wynosi 1/2 miary kąta DAE, czyli 30^o.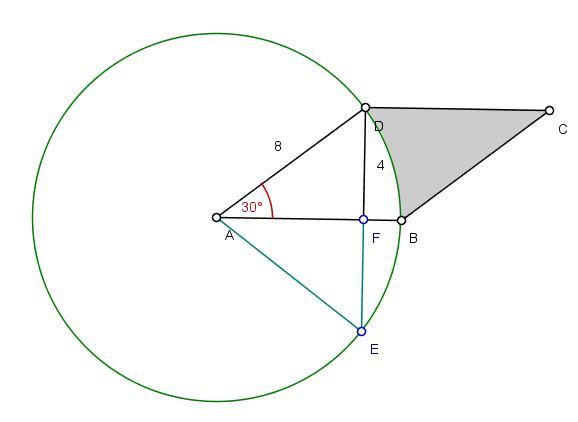

Znając miare kąta DAF możemy obliczyć pole i obwód niezamalowanej figury:
Rysujemy okrąg o promieniu AD (AD=AB), o środku A.
Następnie obliczamy pole wycinka koła o mierze 30^o: 30^o*pr²/360^o=pr²/12=64p/12=16p/3
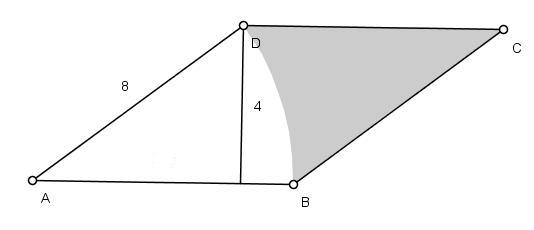
Pole całej figury przedstawionej na rys. do zadania: (8+8)*4/2=32
Teraz możemy obliczyć pole zakreskowanej figury odejmując do pola całego równoległoboku pole nie zakreskowanej figury:32-16p/3 [j²]

Obwód zakreskowanej figury wynosi: 8+8+2pr/12=16+4/3*p[j]

Pole zakreskowanej figury wynosi: (32 - 16p/3) j², a obwód (16+4/3p) j