|
LIGA ZADANIOWA UMK W TORUNIU
ZADANIA W ROKU SZKOLNYM 2009/2010
Zadania przygotowawcze na I spotkanie etapu rejonowego
w dniu 21.11.2009 r.
|
|
|
Tematyka:
1. Działania na liczbach wymiernych.
2. Podzielność liczb naturalnych i całkowitych.
3. Proste obliczenia procentowe.
4. Graniastosłupy.
|
| Zadanie 1 |
Oblicz: 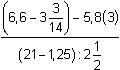 . .
|
| Zadanie 2 |
Wyznacz liczbę dzielników naturalnych liczby
35 + 36 + 37 + 38.
|
| Zadanie 3 |
Podaj 2008 cyfrę rozwinięcia dziesiętnego ułamka  . .
|
| Zadanie 4 |
Czy liczba 666...6, w której cyfra 4 powtarza się 2008 razy jest kwadratem liczby naturalnej?
|
| Zadanie 5 |
Połowa pasażerów, którzy wsiedli do tramwaju na przystanku początkowym zajęła miejsca siedzące. Na pierwszym przystanku liczba pasażerów zwiększyła się o 8%. Ilu pasażerów wsiadło do tramwaju na przystanku początkowym, jeśli wiadomo, że w tramwaju mieści się co najwyżej 70 osób?
|
| Zadanie 6 |
Czy istnieją dwie kolejne liczby naturalne, których sumy cyfr są podzielne przez 11?
|
| Zadanie 7 |
Podaj 2009 cyfrę rozwinięcia dziesiętnego ułamka 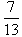 . .
|
| Zadanie 8 |
Ile jest liczb naturalnych mniejszych od 2007, z których żadna nie jest podzielna przez 9, ani przez 19?
|
| Zadanie 9 |
Czy liczba 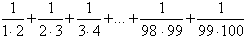 jest większa od jest większa od 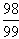 ? ?
|
| Zadanie 10 |
Czy liczba 999...9, w której cyfra 9 powtarza się 2008 razy jest kwadratem liczby naturalnej?
|
| Zadanie 11 |
Wyznacz liczbę dzielników naturalnych liczby 25 + 24 × 33 + 22 × 32.
|
| Zadanie 12 |
Zbadaj, który z ułamków jest większy: 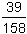 czy 0,24(5) ? czy 0,24(5) ?
|
| Zadanie 13 |
Oblicz 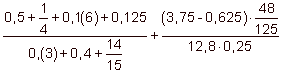 . .
|
| Zadanie 14 |
Wyznacz sumę:
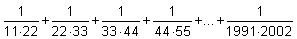 . .
|
| Zadanie 15 |
Wyznaczyć wszystkie liczby pięciocyfrowe mające zapis dziesiętny abcde, które są podzielne przez 36 i dla których a<b<c<d<e.
|
| Zadanie 16 |
Ile istnieje trzycyfrowych liczb przy zapisie których użyto tylko raz cyfry 5?
|
| Zadanie 17 |
2002 jest liczbą palindromiczną tzn., że czytana z lewej strony do prawej i odwrotnie z prawej do lewej jest tą samą liczbą. Poprzednią liczbą palindromiczną jest 1991. Jaka jest maksymalna odległość pomiędzy dwiema kolejnymi liczbami palindromicznymi zawartymi wśród liczb od 1000 do 9999?
|
| Zadanie 18 |
Ile jest liczb naturalnych mniejszych od 2009, z których żadna nie jest podzielna przez 3 ani przez 17?
|
| Zadanie 19 |
W przykładzie zapisanym na tablicy klasowy dowcipniś zmienił dwie cyfry i otrzymano zapis:
4 × 5 × 4 × 5 × 4 = 2247.
Odtwórz pierwotny zapis.
|
| Zadanie 20 |
Czy wśród liczb od 1 do 2002 włącznie więcej jest liczb podzielnych przez 3, czy też liczb, które dzielą się przez 4 lub przez 5?
|
| Zadanie 21 |
Buty kosztujące 100 zł przeceniono o 20%. Po miesiącu, w związku z sezonową obniżką cen, wszystkie ceny zmniejszono o 20 %, a po kolejnym miesiącu dokonano następnej przeceny i wtedy buty kosztowały 60 zł. O ile procent była ostatnia obniżka?
|
| Zadanie 22 |
Czy można znaleźć 55 różnych liczb dwucyfrowych takich, że wśród nich nie ma liczb dających w sumie 100?
|
| Zadanie 23 |
W graniastosłupie liczba krawędzi jest o 2002 większa od liczby ścian. Ile wierzchołków ma ten graniastosłup i jaki wielokąt jest jego podstawą?
|
| Zadanie 24 |
Oblicz:
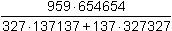 , ,
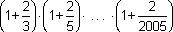 . .
|
Zadanie 25
Reszta z dzielenia liczby pierwszej przez 21 jest liczbą złożoną. Jakie liczby mogą być takimi resztami?
|
| Zadanie 26 |
Każdy z następujących ułamków przedstaw w postaci ułamka zwykłego:
| a) | 0,7(3) |
b) | 0,(134) |
c) | 0,22(13) |
d) | 0,(2002) |
e) | 0,123(144) |
|
| Zadanie 27 |
Dwa prostopadłościenne pudełka mają równe objętości. Jedno z nich ma 1,2 dm wysokości i pole podstawy wynoszące 4,8 dm2. Obliczyć wysokość drugiego pudełka, jeżeli pole jego postawy jest równe 3,6 dm2.
|
| Zadanie 28 |
Czy istnieją dwie kolejne liczby naturalne, których sumy cyfr są podzielne przez 101?
|
| Zadanie 29 |
Mydło w kształcie prostopadłościanu po pewnym czasie zmniejszyło swoje wymiary do połowy. Ile razy większą objętość miało to mydło przed zmydleniem?
|
| Zadanie 30 |
Długość wszystkich krawędzi sześcianu jest równa 76,8 cm. Oblicz objętość tego sześcianu.
|
| Zadanie 31 |
Na giełdzie jedna akcja przedsiębiorstwa SPADEK miała wartość 300 zł. W pierwszej połowie roku cena spadła o 10%, w drugiej wzrosła o 10%. Ile złotych obecnie trzeba zapłacić za 100 akcji tego przedsiębiorstwa?
|
| Zadanie 32 |
Na konto pana Zbyszka wpłynęła jego pensja netto w wysokości 2000 zł. Podatek i inne obciążenia były równe 48% pensji brutto. Ile złotych brutto zarabia pan Zbyszek?
|
| Zadanie 33 |
Połowa zadań to zadania trudne, a połowa zadań to zadania nudne. Ile procent zadań trudnych stanowią zadania nudne, jeśli co trzecie z zadań nudnych to zadanie trudne?
|
| Zadanie 34 |
Bogacz posiadając 100 000 złotych, aby wesprzeć biedaka mającego tylko złotówkę, dał biedakowi 100 złotych. O ile procent zbiedniał bogacz? O ile procent wzbogacił się biedak?
|
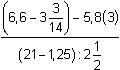 .
.
 .
.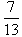 .
.
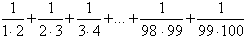 jest większa od
jest większa od 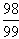 ?
?
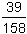 czy 0,24(5) ?
czy 0,24(5) ?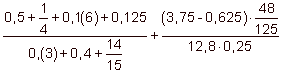 .
.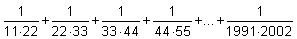 .
. 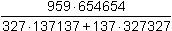 ,
,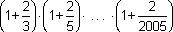 .
.