|
LIGA ZADANIOWA UMK W TORUNIU
ZADANIA W ROKU SZKOLNYM 2009/2010
Zadania przygotowawcze na III spotkanie etapu rejonowego w dniu 13.02.2010 r
dla uczniów klas I gimnazjum
|
|
|
Tematyka:
- Zadania logiczne.
- Proste równania i nierówności prowadzące do zadań tekstowych.
- Układ współrzędnych - figury geometryczne.
|
| Zadanie 1 |
Z podanego wzoru 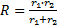 wyznacz r1, a następnie oblicz wartość r1, jeśli R = 2,5 oraz wyznacz r1, a następnie oblicz wartość r1, jeśli R = 2,5 oraz 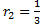 . .
|
| Zadanie 2 |
Piotr i Zbyszek chodzą do tej samej klasy, w której dziewczęta stanowią nie mniej niż 93% i nie więcej niż 94% ogółu uczniów klasy. Ile osób liczy klasa, jeżeli wiadomo, że dziewcząt jest mniej niż 38, a różnica między ilością dziewcząt i chłopców jest liczbą pierwszą
|
| Zadanie 3 |
Dla jakich wartości m, z odcinków 2m + 2, m + 8, 3m + 1, można zbudować trójkąt równoramienny?
|
| Zadanie 4 |
Adam mówi do Tomka: Mam 3 razy więcej lat niż Ty miałeś wtedy, kiedy ja miałem tyle lat ile masz teraz. Kiedy osiągniesz mój obecny wiek będziemy mieli łącznie 112 lat. Ile lat ma obecnie Adam?
|
| Zadanie 5 |
Liczby x, y spełniają równanie 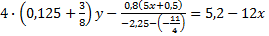 .
Dla jakich x liczba y jest większa od 0,4 liczby x? .
Dla jakich x liczba y jest większa od 0,4 liczby x?
|
| Zadanie 6 |
Lis jest oddalony od psa o 60 swoich skoków. Trzy susy psa to 7 skoków lisa. W ciągu tego samego czasu pies wykonuje 6 susów, a lis 9 skoków. Po ilu susach pies dogoni lisa?
|
| Zadanie 7 |
Dziadek i babcia mają razem 140 lat. Po ile lat ma każde z nich, jeżeli dziadek ma dwa razy tyle lat ile babcia miała wtedy, gdy dziadek miał tyle lat ile ma teraz babcia?
|
| Zadanie 8 |
Sześcienny metalowy klocek o krawędzi 10 cm waży 8 kg. Jaką długość ma krawędź klocka sześciennego ważącego 1 kg i wykonanego z tego samego materiału?
|
| Zadanie 9 |
"Która jest teraz godzina" - pyta Michał ojca.
"A policz: do końca doby pozostało 3 razy mniej czasu niż upłynęło od jej początku."
Która jest teraz godzina?
|
| Zadanie 10 |
Na stadionie, którego bieżnia ma 400 m długości odbył się bieg na 10 km. Zwycięzca ukończył bieg po 30 minutach, a ostatni zawodnik po 32 minutach. Po ilu okrążeniach zwycięzca zdublował ostatniego zawodnika? Przyjmij, że każdy zawodnik biegł ze stałą prędkością.
|
| Zadanie 11 |
Wśród 21 monet jednakowych z wyglądu jedna jest cięższa od pozostałych. W jaki sposób można ją
wykryć przy pomocy trzech ważeń na wadze szalkowej bez odważników?
|
| Zadanie 12 |
Wilgotność skoszonej trawy wynosi 60%, a wilgotność siana równa się 15%. Ile siana otrzyma się z jednej tony trawy?
|
| Zadanie 13 |
Oblicz pole trójkąta ABC, gdzie A = -4,1), B = (-1,4), C = (-5,8).
|
| Zadanie 14 |
Wśród dziewięciu monet jednakowych z wyglądu jedna jest fałszywa (ma inną wagę niż pozostałe monety). Przy pomocy ilu ważeń na wadze szalkowej potrafisz wykryć tę monetę?
|
| Zadanie 15 |
Średni wiek zawodniczek sekcji gimnastycznej wynosi 11 lat. Najstarsza zawodniczka ma 17 lat, średni wiek pozostałych (bez najstarszej) jest równy 10 lat. Ile zawodniczek jest w tej sekcji gimnastycznej?
|
| Zadanie 16 |
Zmniejszając pewną liczbę naturalną o 1, zmniejszamy ją o więcej niż 16,5%. Powiększając zaś tę liczbę o 2, powiększamy ją o mniej niż 33,5%. Wyznacz tę liczbę.
|
| Zadanie 17 |
W stadzie jest 8 owiec. Pierwsza owca zjada stóg siana w ciągu jednego dnia, druga w ciągu dwóch dni, trzecia w ciągu trzech dni, i tak dalej, ósma w ciągu ośmiu dni. Kto szybciej zje stóg siana: dwie pierwsze owce razem, czy wszystkie pozostałe owce razem?
|
| Zadanie 18 |
Teofil i młodsza od niego Agata mają razem 105 lat. Różnica ich wieku równa się liczbie lat Agaty, wtedy, gdy Teofil miał tyle lat, ile teraz ma Agata. Ile lat ma obecnie Agata, a ile Teofil?
|
| Zadanie 19 |
Mianownik ułamka jest o 2010 większy od licznika. Ułamek ten skrócono i otrzymano 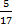 . Znajdź postać tego ułamka przed skróceniem. . Znajdź postać tego ułamka przed skróceniem.
|
| Zadanie 20 |
Cena biletu na mecz piłki nożnej wynosiła 15 zł. Gdy ceną obniżono okazało się, że na mecz przychodzi o 50% widzów więcej, a dochód ze sprzedaży wzrósł o 25%. O ile obniżono ceną biletu?
|
| Zadanie 21 |
Oblicz pole czworokąta ABCD. Jeśli A = (-2,-3) , B = (7,-4), C = (1,1), D = (-1,7).
|
| Zadanie 22 |
Punkty A = (-1,1) , B = (7,1) i C = (2,3) są wierzchołkami trójkąta. Znajdź punkt D taki, że trójkąty ABC i ABD są przystające i C ą D. Rozpatrz wszystkie możliwości.
|
| Zadanie 23 |
Jedna liczba jest większa od drugiej o 406. Jeżeli podzielimy większą liczbę przez mniejszą, to otrzymamy 6 i resztę 66. Wyznacz te liczby.
|
| Zadanie 24 |
Jedna z osób A, B, C, D ukradła brylant. Każda z podejrzanych osób złożyła zeznanie ale tylko jedno z tych zeznań było prawdziwe. Zeznanie A: "Ja nie ukradłem brylantu." Zeznanie B: "A kłamie." Zeznanie C: "B kłamie." Zeznanie D: "B ukradł brylant." Kto powiedział prawdę?
|
| Zadanie 25 |
Pewną działkę Piotr przekopie w ciągu 12 godzin, Zbyszek w ciągu 10 godzin, a Michał w ciągu 8 godzin. W jakim czasie przekopią tę działkę pracując razem?
|
| Zadanie 26 |
Punkty A, B, C, gdzie A = -3,-1), B = (3,-1), C = (1,3), są wierzchołkami pewnego równoległoboku. Jakie współrzędne ma czwarty wierzchołek? Czy wśród równoległoboków są romby i prostokąty?
|
| Zadanie 27 |
Pewien człowiek miał przeprawić się przez rzekę z wilkiem, kozą i kapustą. Łódka, którą znalazł, może zabrać jedno ze zwierząt lub kapustę. Jak mają pokonać rzekę, aby wszyscy w dobrym stanie znaleźli się na drugim brzegu?
|
| Zadanie 28 |
Na jednej z wysp rycerze mówią zawsze prawdę, a giermkowie zawsze kłamią. Pewien człowiek wypowiedział zdanie: Jestem kłamcą. Czy jest mieszkańcem tej wyspy?
|
| Zadanie 29 |
Asię, Bożenkę, Grażynkę poczęstowano w gościnie trzema rodzajami ciast: sernikiem, makowcem i orzechowcem. Każdą z nich innym rodzajem ciasta. Asia nie lubi sernika, Bożenka makowca, Grażynka zaś jest uczulona na orzechy. Na ile sposobów można podzielić te ciasta między dziewczynki tak, aby były zadowolone?
|
| Zadanie 30 |
Zaznacz w układzie współrzędnych punkty A = (-3,2) , B = (4,-2).Znajdź taki punkt C, aby trójkąt ABC był:
- prostokątny o polu 10,5,
- równoramienny i miał pole 21,
- rozwartokątny i miał pole 14.
|
| Uwaga : Dodatkowe zadania przygotowawcze można znaleźć w książce "Liga Zadaniowa".
|
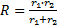 wyznacz r1, a następnie oblicz wartość r1, jeśli R = 2,5 oraz
wyznacz r1, a następnie oblicz wartość r1, jeśli R = 2,5 oraz 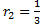 .
.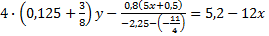 .
Dla jakich x liczba y jest większa od 0,4 liczby x?
.
Dla jakich x liczba y jest większa od 0,4 liczby x?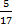 . Znajdź postać tego ułamka przed skróceniem.
. Znajdź postać tego ułamka przed skróceniem.