|
LIGA ZADANIOWA UMK W TORUNIU
ZADANIA W ROKU SZKOLNYM 2009/2010 |
Zadania przygotowawcze III spotkanie etapu rejonowego w dniu 13.02.2010 r
dla uczniów klas II gimnazjum
|
Tematyka:
- Twierdzenie Pitagorasa z zastosowaniami.
- Działania na wyra Zeniach algebraicznych.
- Symetrie w układzie współrzędnych.
|
| Zadanie 1 |
W trójkącie ABC niech D będzie środkiem boku BC. Oblicz pole trójkąta ABC wiedząc, że |AB| = 8 cm, |BC| = 12 cm i |AD| = 10 cm.
|
| Zadanie 2 |
Wyrażenie 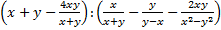 sprowadź do najprostszej postaci i oblicz jego wartość dla sprowadź do najprostszej postaci i oblicz jego wartość dla 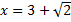 i i 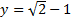 . .
|
| Zadanie 3 |
Środkiem sześciokąta foremnego jest punkt (2, 2), a jednym z jego wierzchołków jest punkt (2, 6). Wyznaczyć pozostałe wierzchołki sześciokąta oraz obliczyć jego pole i obwód.
|
| Zadanie 4 |
Obliczyć odległość między środkami okręgów wpisanego i opisanego dla trójkąta, którego boki
mają długości 30, 30, 48.
|
| Zadanie 5 |
Obliczyć: 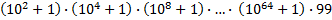 . .
|
| Zadanie 6 |
W trójkącie ABC poprowadzono dwusieczną AD. Wyznaczyć kąty trójkąta ABC, jeśli środek okręgu wpisanego w trójkąt ABD jest jednocześnie środkiem okręgu opisanego na trójkącie ABC.
|
| Zadanie 7 |
Obliczyć wartość wyrażenia (102 + 1).(104 + 1).(108 + 1). ... .(1064 + 1) . 99
|
| Zadanie 8 |
Obliczyć 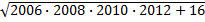
|
| Zadanie 9 |
W trapezie ABCD podstawami są AB i CD, natomiast ramię AD
jest równe sumie podstaw AB i CD. Udowodnić, że dwusieczne kątów wewnętrznych przy wierzchołkach A i D przecinają się na ramieniu BC.
|
| Zadanie 10 |
Wyznacz pole i obwód trójkąta prostokątnego, w którym długość promienia okręgu wpisanego jest równa 4 cm i długość promienia okręgu opisanego jest równa 16 cm .
|
| Zadanie 11 |
Wyznacz pole i obwód
trójkąta prostokątnego, w którym długość promienia okręgu wpisanego jest równa
4 cm i długość promienia okręgu opisanego jest równa 16 cm .
|
| Zadanie 12 |
Wyznacz pole i obwód trójkąta prostokątnego , w którym wysokość poprowadzona z wierzchołka kąta prostego dzieli przeciwprostokątną na odcinki długości 2 cm i 8 cm .
|
| Zadanie 13 |
Wyznacz pole ośmiokąta, w którym wszystkie kąty wewnętrzne są równe, zaś boki maja długości 2, 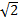 , 2, , 2, 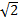 , 2, , 2, 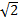 , 2, , 2, 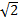 . .
|
| Zadanie 14 |
Środkiem symetrii rombu jest punkt (0, 0). Jednym z jego wierzchołków jest punkt (2,-2). Wyznacz współrzędne pozostałych wierzchołków tego rombu, jeśli jego pole wynosi 8.
|
| Zadanie 15 |
W trójkącie prostokątnym ABC, w którym 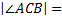 900, poprowadzono wysokość CD. Niech r będzie promieniem okręgu wpisanego w trójkąt ADC, r1 - promieniem okręgu wpisanego w trójkąt ADC, r2 - promieniem okręgu wpisanego w trójkąt BCD. Udowodnić, że r + r1 + r2 = |CD|. 900, poprowadzono wysokość CD. Niech r będzie promieniem okręgu wpisanego w trójkąt ADC, r1 - promieniem okręgu wpisanego w trójkąt ADC, r2 - promieniem okręgu wpisanego w trójkąt BCD. Udowodnić, że r + r1 + r2 = |CD|.
|
| Zadanie 16 |
Obliczyć odległość między środkami okręgów wpisanego i opisanego dla trójkąta, którego boki
maja długości 20, 20, 32.
|
| Zadanie 17 |
Obliczyć wartość wyrażenia:
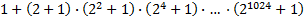 , ,
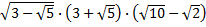 , ,
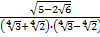 . .
|
| Zadanie 18 |
Przedstawić w najprostszej postaci:
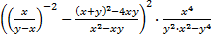 , ,
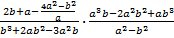 , ,
|
| Zadanie 19 |
Bok prostokąta ma długość 24 cm, a jego przekątna ma długość 26 cm. Przekątna
dzieli prostokąt na dwa trójkąty. Każdy z nich wpisujemy koło. Oblicz odległość między środkami tych kół.
|
| Zadanie 20 |
Środkiem sześciokąta foremnego jest punkt (-1, -1), a jednym z jego wierzchołków jest punkt (-5, -1). Wyznaczyć pozostałe wierzchołki sześciokąta oraz obliczyć jego pole i obwód.
|
| Zadanie 21 |
Uzasadnij, że w trójkącie prostokątnym suma d długości w przyprostokątnych jest równa sumie
średnic okręgu wpisanego i opisanego na tym trójkącie.
|
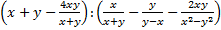 sprowadź do najprostszej postaci i oblicz jego wartość dla
sprowadź do najprostszej postaci i oblicz jego wartość dla 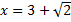 i
i 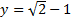 .
.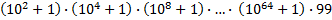 .
. 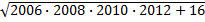
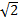 , 2,
, 2, 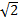 , 2,
, 2, 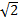 , 2,
, 2, 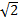 .
.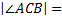 900, poprowadzono wysokość CD. Niech r będzie promieniem okręgu wpisanego w trójkąt ADC,
900, poprowadzono wysokość CD. Niech r będzie promieniem okręgu wpisanego w trójkąt ADC, 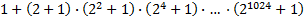 ,
,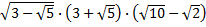 ,
,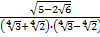 .
.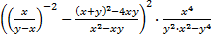 ,
,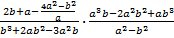 ,
,