|
LIGA ZADANIOWA UMK W TORUNIU
ZADANIA W ROKU SZKOLNYM 2009/2010 |
Zadania niespodzianki
dla uczniów klas II gimnazjum
na zakończenie konkursu 2009/2010
|
| Zadanie 1 |
| Udowodnić, że jeśli p jest liczbą pierwszą większą niż 1000, to można w jej zapisie wykreślić jedną lub dwie cyfry tak, aby otrzymać liczbę pierwszą.
|
| Zadanie 2 |
Zapis dziesiętny liczby 5.A składa się z 100 piątek i 100 szóstek. Znaleźć sumę cyfr liczby A.
|
| Zadanie 3 |
Na tablicy zapisano 9 kolejnych liczb trzycyfrowych, w zapisie których nie występuje cyfra 0. W każdej liczbie obliczono iloczyn cyfr, a następnie iloczyny te zsumowano. Czy jest możliwe aby suma tych iloczynów była równa 1125?
|
| Zadanie 4 |
| Liczba sześciocyfrowa dzieli się przez 8. Jaką największą sumę cyfr może ona mieć?
|
| Zadanie 5 |
W trójkącie ABC poprowadzono środkową AM i wysokość BH. Obliczyć |BC|, jeśli wiadomo, że |AH| = 1 i 2|<MAC|=|<MCA|.
|
| Zadanie 6 |
Czy można z prostokątów 1×1, 1×2, 1×3, ..., 1×13 złożyć prostokąt?
|
| Zadanie 7 |
Mamy 1001 jednakowo wyglądających monet. Wiadomo, że wśród nich jest tylko jedna fałszywa - ma inną wagę od pozostałych. Wyjaśnij przy pomocy dwóch ważeń na wadze szalkowej bez odważników czy moneta fałszywa jest cięższa czy lżejsza od pozostałych monet.
|
| Zadanie 8 |
Piotr, Zbyszek i Mirek mają łącznie 100 zadań z pewnego zestawu, przy czym każdy z nich rozwiązał 60 zadań. Zadanie uważamy za "trudne" jeżeli rozwiązał je tylko jeden z chłopców, natomiast zadanie uważamy za "łatwe "jeżeli rozwiązali je wszyscy chłopcy. Pozostałe rozwiązane zadania uważamy za "średnie". Uzasadnij, że zadań trudnych było o 20 więcej niż zadań łatwych.
|
| Zadanie 9 |
Na okręgu mamy 10 punktów. Na zmianę każdy z dwóch chłopców łączy dwa punkty spośród danych odcinkiem. Który z chłopców może zapewnić sobie wygraną, jeśli nie wolno tych samych punktów łączyć ponownie, natomiast odcinki mogą się przecinać, mieć punkty wspólne. Przegrywa ten, który nie może poprowadzić odcinka. Który z chłopców ma strategię wygrywającą?
|
| Zadanie 10 |
Iloczyn pewnej liczby naturalnej przez sumę jej cyfr jest równy 2008. Wyznaczyć wszystkie liczby o tej własności.
|
| Zadanie 11 |
Czy prawdą jest, że do każdej liczby naturalnej równej iloczynowi dwóch kolejnych liczb naturalnych można dopisać z prawej strony dwie cyfry tak, aby otrzymać liczbę będącą kwadratem liczby
naturalnej?
|
| Zadanie 12 |
Na tablicy napisano następujące liczby 1, 2, 4, 8, 16, 23, 28, . . . itd. Każda kolejna liczba, począwszy od drugiej, powstaje z poprzedniej przez dodanie do niej sumy jej cyfr. Czy na tablicy pojawi
się liczba 200720082009?
|
| Zadanie 13 |
Obliczyć 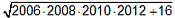 . .
|
| Zadanie 14 |
Czy istnieją takie cyfry a i b, gdzie b > a, dla których liczba 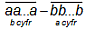 jest liczbą pierwszą?
jest liczbą pierwszą?
|
| Zadanie 15 |
Wyznaczyć wszystkie liczby naturalne a, dla których dwa zdania spośród poniższych trzech będą prawdziwe, a jedno fałszywe:
- a + 41 jest kwadratem liczby naturalnej.
- a − 21 jest liczbą podzielną przez 10.
- a − 48 jest kwadratem liczby naturalnej.
|
| Zadanie 16 |
W trapezie ABCD podstawami są AB i CD, natomiast ramię AD jest równe sumie podstaw AB i CD. Udowodnić, że dwusieczne kątów wewnętrznych przy wierzchołkach A i D przecinają się na ramieniu BC.
|
| Zadanie 17 |
Na trójkącie równobocznym ABC opisano okrąg. Na łuku BC nie przechodzącym przez punkt A wybrano punkt P, różny od końców łuku. Odcinki AP i BC przecinają się w punkcie K. Wykazać, że 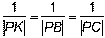 . .
|
| Zadanie 18 |
W sali kinowej mamy 7 rzędów po 10 miejsc w każdym rzędzie. Na poranny seans przyszła
grupa 50 uczniów. Ta sama grupa przyszła do tej sali na popołudniowy seans. Udowodnić, że w tej
grupie znajdzie się dwoje dzieci, które zarówno na porannym seansie jak i na popołudniowym seansie
siedziały w tym samym rzędzie (niekoniecznie o tym samym numerze, np. rano mogły siedzieć w
rzędzie o numerze 1, a po południu w rzędzie o numerze 5).
|
| Zadanie 19 |
Wyznaczyć największy wspólny dzielnik liczb a = 22008 − 1 i b = 22009 + 1.
|
| Zadanie 20 |
Wyznaczyć 2009 liczb naturalnych takich, że suma tych liczb jest równa ich iloczynowi.
|
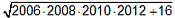 .
. 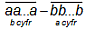 jest liczbą pierwszą?
jest liczbą pierwszą?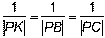 .
.