|
LIGA ZADANIOWA UMK W TORUNIU
ZADANIA W ROKU SZKOLNYM 2009/2010
Zadania niespodzianki
dla uczniów szkół podstawowych
na zakończenie konkursu 2009/2010
|
| Zadanie 1 |
Ile liczb między 1 i 100 zawiera cyfrę 5?
|
| Zadanie 2 |
Największym średniowiecznym dzwonem w Polsce jest zawieszony na wieży katedry św. Janów w Toruniu Tuba Dei. Zazwyczaj materiałem do wykonania dzwonów jest odmiana brązu cynowego, tzw. spiż (stop o następujących proporcjach: ok. 0,8 miedzi i ok. 0,2 cyny, do którego czasem dodaje się niewielkie ilości srebra i złota).
Toruński Tuba Dei pochodzący z 1500 r. waży około 7,5 t. Masa krakowskiego dzwonu Zygmunt wynosi około 10,9 t.
Oblicz, ile ton miedzi zawiera Tuba Dei.
- O ile procent cięższy jest Zygmunt od Tuba Dei?
- O ile procent lżejszy jest Tuba Dei od Zygmunta?
- Jaka byłaby masa dzwonu zawierającego 350 kg cyny?
|
 |
| Zadanie 3 |
Iloczyn liczby naturalnej przez sumę jej cyfr wynosi 2008. Wyznaczyć wszystkie liczby o tej własności.
|
| Zadanie 4 |
W ilu dwucyfrowych liczbach suma cyfr jest wielokrotnością 6?
|
| Zadanie 5 |
Ile różnych rozwiązań ma to dzielenie OSA : TO = AO? Różne litery zastępują różne cyfry oraz żadna liczba nie zaczyna się od zera.
|
| Zadanie 6 |
Na pewnym zebraniu było stu polityków. Każdy z nich był uczciwy bądź nieuczciwy.
Znamy dwa fakty:
- Co najmniej jeden z polityków był uczciwy.
- Co najmniej jeden z dwóch dowolnych polityków był nieuczciwy.
Czy znając te fakty można powiedzieć ilu polityków było uczciwych, a ilu nieuczciwych?
|
| Zadanie 7 |
| W koszyku są piłeczki zielone, czerwone i niebieskie, razem 46. Zielonych piłeczek
jest tyle samo, co czerwonych i niebieskich razem, czerwonych jest o 5 mniej niż niebieskich. Ile piłeczek każdego koloru jest w koszyku? |
| Zadanie 8 |
Mamy 8 odcinków, których długości są liczbami całkowitymi centymetrów. Najdłuższy z nich ma długość 20 cm. Udowodnij, że istnieją wśród nich 3 odcinki, z których można zbudować trójkąt.
|
| Zadanie 9 |
Mamy naczynie o pojemności 24 litry pełne wody i 3 puste naczynia o pojemności 13,11 i 5 litrów. Podziel wodę na trzy równe części. Spróbuj to wykonać, przelewając jak najmniej razy.
|
| Zadanie 10 |
Mamy 4 podobne monety. Trzy z nich ważą po 5 g, a masa czwartej monety jest różna od tych trzech. Jak za pomocą wagi i jednego odważnika o masie 5 g ważąc dwa razy, znaleźć fałszywą monetę i ustalić czy jest ona cięższa czy lżejsza od pozostałych?
|
| Zadanie 11 |
Karton o wymiarach 30 cm na 21 cm trzeba pociąć tak, aby otrzymać jak najwięcej biletów o wymiarach 6cm na 8 cm. Ile można wyciąć takich biletów?
|
| Zadanie 12 |
Na ile sposobów można rozmienić 10 groszówkę?
|
| Zadanie 13 |
Symbol 50! oznacza iloczyn liczb całkowitych od 1 do 50 włącznie. Gdybyś rzeczywiście wykonał to działanie, to ile zer otrzymałbyś na końcu?
|
| Zadanie 14 |
Kartkę papieru o wymiarach 16 cm na 32 cm przecięto na pół. Jedną z tych części przecięto znowu na pól i powtórzono tę czynność tyle razy aż otrzymano prostokąt o wymiarach 1 cm na 2 cm. Ile cięć w sumie wykonano?
|
| Zadanie 15 |
Liczba nadwymiarowa to taka liczba, której suma dzielników właściwych (czyli z wyłączeniem samej liczby) jest większa od niej samej.
Na przykład, dzielnikami właściwymi liczby 8 są 1, 2 i 4, zaś 1 + 2+ 4 to mniej niż 8, a zatem 8 nie jest liczbą nadwymiarową.
Ile jest liczb nadwymiarowych mniejeszych od 30?
|
| Zadanie 16 |
Jedna z 27 monet jest fałszywa i cięższa od innych. Ważąc w ręku nie można jej odróżnić od innych. Jak ustalić, która moneta jest fałszywa, ważąc 3 razy na wadze szalkowej bez odważników?
|
| Zadanie 17 |
W sali kinowej mamy 7 rzędów po 10 miejsc w każdym rzędzie. Na poranny seans przyszła grupa 50 uczniów. Ta sama grupa przyszła do tej sali na popołudniowy seans. Udowodnić, że w tej grupie znajdzie się dwoje dzieci, które zarówno na porannym seansie jak i na popołudniowym seansie siedziały w tym samym rzędzie (niekoniecznie o tym samym numerze, np. rano mogły siedzieć w rzędzie
o numerze 1, a po południu w rzędzie o numerze 5).
|
| Zadanie 18 |
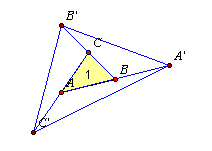 Pole trójkąta ABC równa się 1.
Punkt A' jest symetryczny do A względem B,
punkt B' jest symetryczny do B względem C,
punkt C' jest symetryczny do C względem A.
Oblicz pole trójkąta A'B'C'.
|
| Zadanie 19 |
Mamy do dyspozycji 3 kolory. Na ile sposobów można pomalować ściany sześcianu, używając każdego koloru dwukrotnie, przy czym każda ściana jest pomalowana wyłącznie jednym kolorem?
|
| Zadanie 20 |
Jaka jest 7000-na cyfra po przecinku w rozwinięciu dziesiętnym ułamka 1/7000?
|