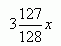 jeśli umowa między dłużnikiem, a wierzycielem zakłada, że pierwsze trzy raty będą jednakowej wysokości, a każda następna będzie równa połowie poprzedniej, oraz że wszystkich rat jest 10
jeśli umowa między dłużnikiem, a wierzycielem zakłada, że pierwsze trzy raty będą jednakowej wysokości, a każda następna będzie równa połowie poprzedniej, oraz że wszystkich rat jest 10LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 4
Zapisz i doprowadź do najprostrzej postaci wyrażenie algebraiczne,na którego podstawie można obliczyć kwotę spłaconych pieniędzy, jeśli umowa między dłużnikiem, a wierzycielem zakłada, że pierwsze trzy raty będą jednakowej wysokości, a każda następna będzie równa połowie poprzedniej, oraz że wszystkich rat jest 10.
Rozwiązanie
Pierwszą ratę oznaczę x, a że trzy pierwsze raty są takie same to będzie to wyglądało: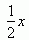
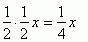
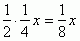
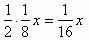
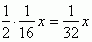
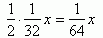
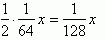
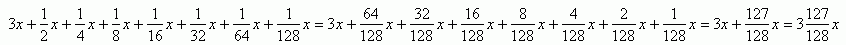
Odpowiedź
Kwota spłaconych pieniędzy wynosi 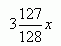 jeśli umowa między dłużnikiem, a wierzycielem zakłada, że pierwsze trzy raty będą jednakowej wysokości, a każda następna będzie równa połowie poprzedniej, oraz że wszystkich rat jest 10
jeśli umowa między dłużnikiem, a wierzycielem zakłada, że pierwsze trzy raty będą jednakowej wysokości, a każda następna będzie równa połowie poprzedniej, oraz że wszystkich rat jest 10
Agnieszka Biegun