LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM

Zadanie 11

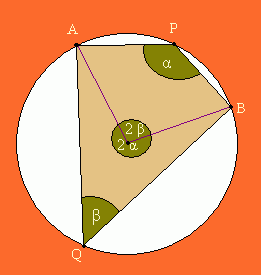
Dany jest okrąg i dwa różne punkty A i B należące do tego okręgu. Na łuku AB obieramy dowlny punkt P (PąA i PąB), a na pozostałej części dowolny punkt Q. Uzasadnij, że suma kątów APB i AQP jest kątem półpełnym.

Rozwiązanie:

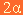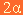Jeżeli z punktów A i B poprowadzimy proste spotykające się w środku okręgu otrzymamy dwa kąty środkowe oparte na łukach AB i BA. Wykorzystując twierdzenie o kącie środkowym i wpisanym możemy zauważyć, że kąty rozmiar: 874 bajtów i rozmiar: 887 bajtów tworzą kąt pełny (360°). Idąc drogą dedukcji na podstawie prostego równania możemy udowodnić, że kąty rozmiar: 850 bajtów i rozmiar: 865 bajtów tworzą kąt półpełny (180°).
rozmiar: 3610 bajtów

Dowód:


rozmiar: 874 bajtów+rozmiar: 887 bajtów=360° /:2
rozmiar: 850 bajtów+rozmiar: 865 bajtów=180°

Małgorzata Hapyn