| a) | 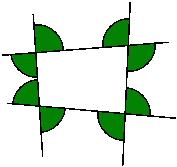 | b) | 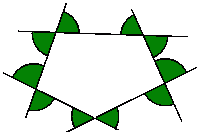 | c) | 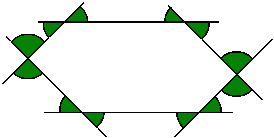 |
LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 13
W każdym z wielokątów poniżej oblicz sumę miar kątów zaznaczonych łukami. Co zauważyłeś?a) 
b) 
c) 
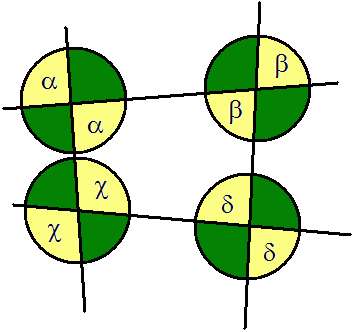
4 × 360° = 1440°
2) Obliczamy, ile wynosi suma miar kątów zaznaczonych na zielono:
1440° - 2 × (a + b + c + d)Ponieważ suma kątów wewnetrznych w czworokącie wynosi 360°, więc:
a + b + c + d = 360°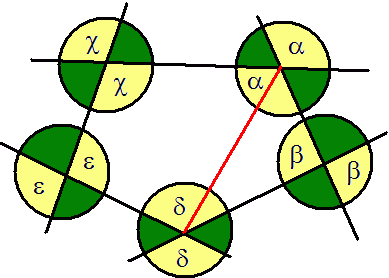
1) Gdybyśmy połączyli dwa naprzeciwległe kąty powstałby czworokąt i przystający do niego trójkąt.
2) Obliczamy ile wynosi suma miar wszystkich kątów zaznaczonych na rysunku:
5 × 360° = 1800°3) Obliczamy sumę miar kątów zaznaczonych na zielono:
1800° - 2 × (a + b + c + d + e)Ponieważ suma kątów wewnętrznych w czworokącie wynosi 360°, a w trójkącie 180°, więc suma tych kątów będzie wynosiła 360° + 180° = 540°
a + b + c + d + e = 540°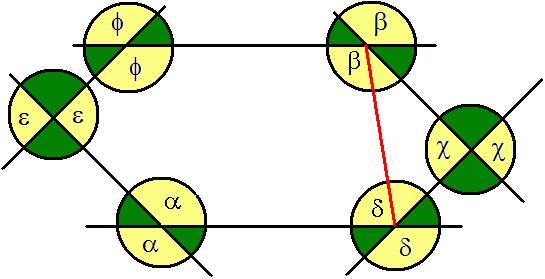
1) Gdybyśmy połączyli dwa naprzeciwległe kąty powstałby pięciokąt i przystający do niego trójkąt.
2) Obliczymy, ile wynosi suma miar wszystkich kątów zaznaczonch na rysunku:
2160° - 6 × 360° = 2160°3) Obliczymy, ile wynosi suma miar kątów zaznaczonych na zielono:
2 × (a + b + c + d + e + f)Ponieważ suma kątów wewnętrznych w pięciokącie wynosi 540°, a w trójkącie 180° więc suma tych kątów wynosi 540° + 180° = 720°)
a + b + c + d + e + f = 720°Dominika Jackowska
kl. I a G