LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 14
Punkty A="(3,4)" i B="(3,10)" są wierzchołkami trójkąta ABC, którego pole jest równe 15 (jednostek kwadratowych). Znajdź wspótłrzędne punktu C, wiedząc, że:
a) trójkąt ABC jest równoramienny i odcinek AB jest jego podstawą
b) trójkąt ABC jest prostokątny
c) druga współrzędna punktu C jest równa: -3
Rozwiązanie
Pole trójkąta wyraża się wzorem:
P = ½ × a × h
P = 15, a = |AB| = 6
15 = ½ × 6 × h
15 = 3 × h
h = 5
a) - ×2 Ţkolor i liczba trójkątów
b) - ×4 Ţkolor i liczba trójkątów
c) - ×2 Ţkolor i liczba trójkątów
Odpowiedź
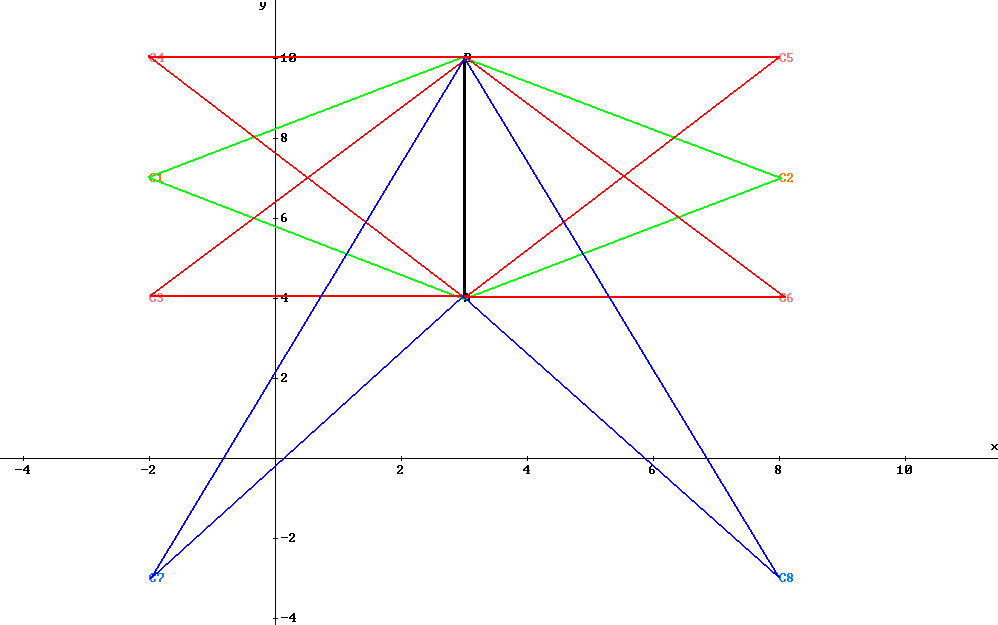
Odp. a) Współrzędne punktu C mogą być równe (-2,7) lub (8,7).
Odp. b) Współrzędne punktu C mogą być następujące: (-2,4), (-2,10), (8,10), (8,4),
Odp c) Współrzędne punktu C mogą być równe (-2,-3) lub (8,-3)
Uzasadnienie
W podpunkcie a trójkąty mają wysokość 5 (jednostek długości) i są równoramienne.
W podpunkcie b trójkąty są prostokątne i mają wysokość = 5.
W podpunkcie c są to jedyne trójkąty, które mają wysokość = 5, a drugą współrzędną punkt C jest -3.
Tomasz Jankowki
kl.Ia
