LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 15
Na okręgu o środku O zaznaczono punkty A, B i C tak, że kąt wpisany ABC ma miarę 40o, a kąt środkowy BOC ma miarę 160o. Oblicz miary kątów w trójkątach AOB, AOC, BOC.
Rozwiązanie
Oto rysunek pomocniczy, na którym będziemy bardzo wiele omawiać.
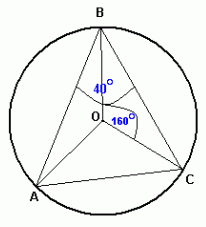
Odcinki ˝AO˝, ˝BO˝ i ˝CO˝ są równe, ponieważ są to promienie okręgu.
Wobec tego wnioskujemy, że:- trójkąty AOB, AOC, BOC są równoramienne
- pary kątów: OAB i OBA, OBC i OCB, OAC i OCA są równe.
Suma miar kątów wewnętrznych w trójkącie = 180o.
Miara kąta OBC i OCB = (180o - 160o) = 10o.
Miara kąta OAB = miara kąta OBA = 40o - 10o = 30o.
Miara kąta AOB = 180o - 2 × 30o = 120o.
Miara kąta AOC = 360o - 160o - 120o = 80o.
Miara kąta OAC = miara kąta OCA = (180o - 80o) : 2 = 50o.
Grzegorz Jóźwiak
Klasa 1ag

