Liga Zadaniowa UMK w Toruniu

Zadanie 16

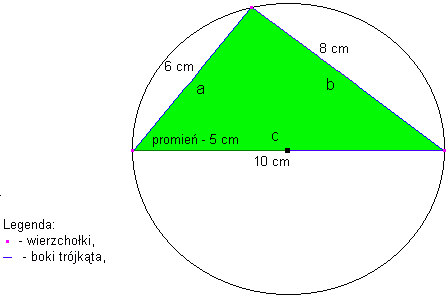
Wierzchołki trójkąta o bokach długości 6 cm, 8 cm i 10 cm leżą na okręgu o promieniu 5cm.Oblicz pole tego trójkąta.

Rozwiązanie:

Sprawdzam czy trójkąt ten jest prostokątny na podstawie twierdzenia odwrotnego do twierdzenia Pitagorasa:

Jeśli kwadrat najdłuższego boku jest równy sumie kwadratów pozostałych boków to trójkąt jest prostokątny i najdłuższy bok jest przeciwprostokątną.

10² = 100

8² + 6² = 64 +36 = 100

8² + 6² = 10²

A więc jest to trójkąt prostokątny. Przyjmijmy oznaczenia tak jak na rysunku:

2. Pole P tego trójkąta jest równe:

P = ½ ab = ½ 6×8 = 24 (cm²)

Odpowiedź: Pole trójkąta wynosi 24 cm²

Joanna Karnowska