LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 22
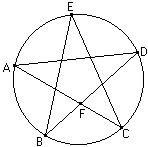
Na rysunku obok punkty A,B,C,D i E dzielą okrąg na równe części.Oblicz miary kątów wpisanego CAD, kąta CDE oraz kąta CFB.
Rozwiązanie
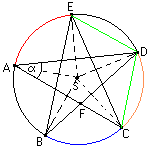
Na początku wyznaczam środek okręgu i oznaczam go literą S. Punkty A,B,C,D,E łączę ze środkiem liniami przerywanymi.Dzięki temu uzyskuję kąty, które dzielą okrąg na 5 równych części, a każdy kąt ma 72°, gdyż
360°:5="72°
Pierwszy szukany kąt CAD oznaczam jako a .Kąt ten oparty jest na łuku CD (zaznaczonym przeze mnie kolorem pomarańczowym), na którym jest również oparty kąt środkowy CSD. Kąt CAD jest kątem wpisanym. Korzystając z twierdzenia o kącie środkowym i wpisanym, które mówi, że kąt środkowy oparty na tym samym łuku co kąt wpisany ma miarę dwa razy większą.Mogę więc obliczyć miarę kątaagdyż jest ona dwa razy mniejsza od miary kąta CSD, który ma 72° co już wcześniej obliczyłam. Wynosi ona w takim razie:
72°:2="36°
Następnie zaznaczam zielonym kolorem kolejny kąt, którego miarę mam obliczyć, czyli CDE. Zauważyłam, że kąt BDA ma taką samą miarę jak kąt CAD, czyli 36°.
Teraz chcę obliczyć miarę kąta BDC,a jest to kąt wpisany oparty na łuku BC, który zaznaczyłam kolorem niebieskim. Na łuku tym oparty jest również kąt środkowy BSC. Dzięki temu mogę obliczyc miarę kąta BDC, korzystając z wcześniej opisanego twierdzenia o kącie srodkowym i wpisanym. Kąt środkowy BSC ma 72°, więc kat BDC ma miarę :
72°:2="36°
Pozostało mi teraz obliczyc miarę kąta EDA, a jest on również kątem wpisanym, tak jak dwa poprzednie. EDA jest oparty na łuku EA, zaznaczonym przeze mnie kolorem czerwonym. Na łuku tym oparty jest także kąt srodkowy ESA, który ma miarę 72°.Kąt EDA ma więc miarę dwa razy mniejsza czyli 36°, tak jak poprzednie kąty. Teraz obliczam miarę kąta CDE, a wynosi ona :
36°+36°+36="108°
Ostatnim kątem, którego miarę mam obliczyć jest CFB. Zauważyłam, że jest to kąt naprzemianległy do kąta DFA, który jest jednym z katów trójkąta DFA. Trójkąt ten jest równoramienny, dzięki czemu mogę obiczyć miarę kąta DFA. Kąty przy ramionach tego trójkata mają po 36°, co wynika z wcześniejszych obliczeń. Zatem kąt DFA ma miarę :
180°-2 36°=180°-72°=108°
Ponieważ kąt CFB jest naprzemianległy do kąta DFA, ma on taka samą miarę, czyli 108°.