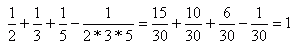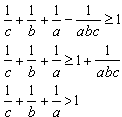LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS II GIMNAZJUM
Zadanie 9
Wyznacz wszystkie trójki liczb pierwszych takie, że iloczyn każdych dwóch z nich przy dzieleniu przez trzecią daje resztę 1.
Rozwiązanie:
Oznaczmy szukane liczby jako a,b,c.
Z założenia wynika, że liczby a, b, c są różne
(bo np. niemozliwe jest żeby a×b przy dzieleniu przez c="a dało resztę 1, gdyż ab dzieli się przez a)
oraz :
(ab-1)/c
(ac-1)/b
(bc-1)/a
są liczbami całkowitymi dodatnimi.
Wiemy , że iloczyn liczb całkowitychdodatnich da nam liczbę całkowitą dodatnią.
No to pomnóżmy te liczby przez siebie:
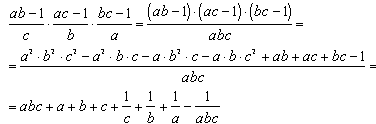
Wynika stąd, że  jest liczbą całkowitą dodatnią.
jest liczbą całkowitą dodatnią.
Wiemy także, że liczba całkowita dodatnia jest liczbą większą lub równą 1. Podstawmy teraz za a 2, za b 3, za c 5:
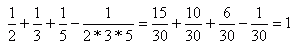
Widzimy, ze taką trójką liczb są liczby 2, 3, 5. Są to także jedyne takie liczby, ponieważ tak jak już wcześniej wspomniałem liczba całkowita dodatnia musi być większa lub równa 1.
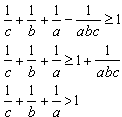
Oznacza to, że
im większy jest mianownik w ułamku, tym mniejszy jest sam ułamek. Jeżeli podstawimu kolejne liczby pierwsze, to ułamki będą się zmniejszały i nie dostaniemy już żadnego wyniku, który byłby większy
lub równy 1.
ODPOWIEDŹ:
Istnieje tylko jedna taka trójka liczb pierwszych, taka że iloczyn każdych dwóch z nich przy dzieleniu przez trzecią daje resztę 1. Są to liczby: 2,3,5.
FILIP IDZIKOWSKI
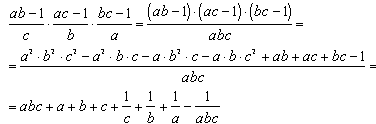
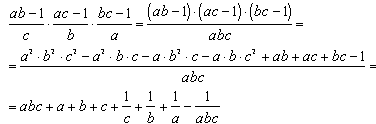
 jest liczbą całkowitą dodatnią.
jest liczbą całkowitą dodatnią.