LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 4
Oblicz miary kątów trójkąta równoramiennego, którego wierzchołki leżą na okręgu wiedząc, że jeden z boków
jest oparty na łuku, którego długość jest równa 1/5 długości całego okręgu.
Rozwiązanie
Możemy rozważyć dwa przypadki:
a) Bok oparty na łuku równym 1/5 okręgu jest ramieniem trójkąta.
b) Bok oparty na łuku równym 1/5 okręgu jest podstawą trójkąta.
a)
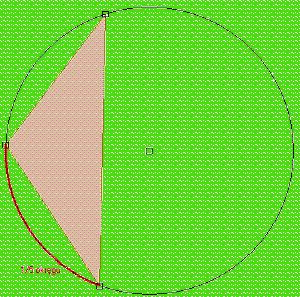(rysunek pomocniczy)
Kąt środkowy oparty na łuku długości okręgu ma miarę 360°, więc kąt środkowy oparty na łuku
długości 1/5 okręgu ma miarę 5 razy mniejszą. 360° ÷ 5 = 72°
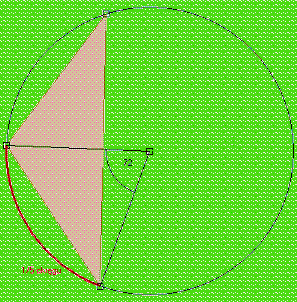
Z twierdzenia o kącie środkowym i wpisanym (kąt środkowy oparty na łuku jest dwa razy większy niż kąt wpisany oparty na tym samym łuku)
wiemy, że kąt wpisany oparty na łuku długości 1/5 okręgu równa się 36° bo 72° ÷ 2 = 36°
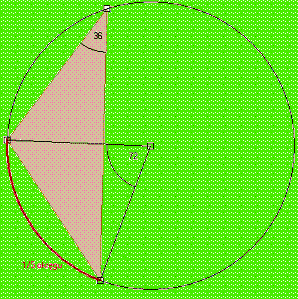
W trójkącie równoramiennym kąty przy podstawie są równe.Miara kątów w trójkącie jest równa 180°. Możemy obliczyć trzeci kąt. 180° 2 ˇ 36 = 108°
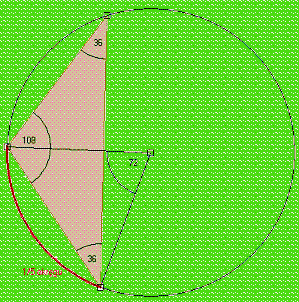
Odp.Miary kątów równają się: 36°, 108°, 36°.
b)
W tym przypadku postępujemy podobnie, tylko kąt 36° nie będzie przy podstawie.
Wtedy pozostałe dwa kąty można łatwo obliczyć.Oznaczmy je x (wiemy, że są równe bo są przy podstawie).
2x = 180° - 36°
2x = 144° /÷2
x = 72°
Odp.Miary kątów równają się: 72°, 36°, 72°.,
Krzysztof Chrzanowski