Z tego wynika, że sześcianem tej liczby będzie
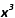 .
.
Wiedząc, że konkretne liczby dają tą samą reszte z dzielenia, ich różnica będzie przez nią podzielna:
PREZENT WAKACYJNY 2006/7
DLA UCZNIÓW GIMNAZJUM
1. Podstawiamy x jako dowolną liczbę naturalną nieparzystą.
Z tego wynika, że sześcianem tej liczby będzie 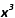 .
.
Wiedząc, że konkretne liczby dają tą samą reszte z dzielenia, ich różnica będzie przez nią podzielna:
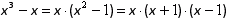
2. Liczba x jest nieparzysta, zatem liczby x+1 i x-1 są kolejnymi liczbami parzystymi. Ponieważ co druga liczba parzysta dzieli się przez 4 więc jedna spośród liczb x+1; x-1 dzieli się przez 2, a druga przez 4
3. Ponad to x-1; x; x+1 są kolejnymi liczbami naturalnymi, więc co trzecia liczba dzieli się przez 3, więc któraś z tych liczb musi dzielić się przez 3
4. Biorąc pod uwage, że ta liczba dzieli się 2×4×3 czyli przez 24, to także dzieli się przez dzielniki liczby 24 tzn 24,12,8,6,4,3,2,1.