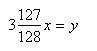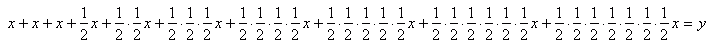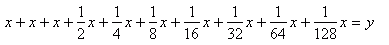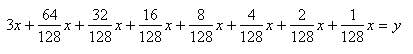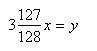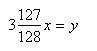LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 8
Zapisz i doprowadź do najprostszej postaci wyrażenie algebraiczne,
na którego podstawie
można obliczyć kwotę spłaconych pieniędzy,
jeśli umowa między dłużnikiem, a wierzycielem
zakłada,
że pierwsze trzy raty będą jednakowej wysokości, a każda następna
będzie równa
połowie poprzedniej, oraz że wszystkich rat jest 10.
Rozwiązanie:
Na początku przyjmuję, takie oznaczenia, że:
x - pierwsza rata spłacanych pieniędzy
y - to cała kwota spłaconych pieniędzy (10 rat)
Teraz zapisuje całe wyrażenie algebraiczne (czyli wszystkie 10 rat):
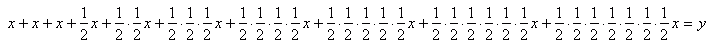
Moim zadaniem jest doprowadzić powyższe wyrażenie do jak najprostszej postaci,
więc najpierw jak najłatwiej przedstawiam każdą z 10 rat, czyli:
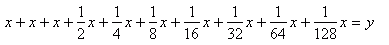
Teraz sprowadzam wszystkie ułamki do wspólnego mianownika:
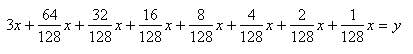
I dodaję..
Po dodaniu wychodzi mi najprostsza postać początkowego wyrażenia algebraicznego.
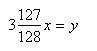
Odp. Najprostszym wyrażeniem algebraicznym, dzięki któremu można obliczyć kwotę spłaconych pieniędzy jest:
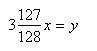
Joanna Jędrzejewska kl.Ia