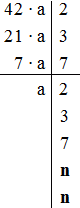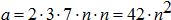PREZENT WAKACYJNY 2006/7
DLA UCZNIÓW GIMNAZJUM
Zadanie 8
Wypisano po kolei siedem różnych liczb naturalnych w jednym wierszu.
Iloczyn każdych
dwóch kolejnych (sąsiednich) liczb jest kwadratem liczby naturalnej.
Pierwszą liczbą jest 42.
Udowodnij, że przynajmniej jedna z tych liczb jest większa niż 2007.
Rozwiązanie:
1. Na początek przyjmijmy takie oznaczenia:
a - druga liczba wypisana w wierszu
b - trzecia liczba wypisana w wierszu
c - czwarta liczba wypisana w wierszu
d - piąta liczba wypisana w wierszu
e - szósta liczba wypisana w wierszu
f - szósta liczba wypisana w wierszu
Czyli wygląda to tak: 42, a, b, c, d, e - sześć różnych liczb naturalnych wypisanych po kolei.
2. Jeśli liczba jest kwadratem liczby naturalnej, to w rozkładzie na czynniki pierwsze,
każdy czynnik musi wystąpić parzystą ilość razy.
3. Iloczyn liczby 42 i a ma być kwadratem liczby naturalnej tzn.,
że w rozkłądzie na czynniki liczby a powinny wystąpić: 2, 3, 7.
Ponieważ 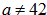 , więc w rozkładzie powinien wystąpić (dwukrotnie) jeszcze jeden
czynnik, który oznaczę literą n.
, więc w rozkładzie powinien wystąpić (dwukrotnie) jeszcze jeden
czynnik, który oznaczę literą n.
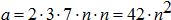
4. Podobnie dla pozostałych liczb:
| 42 |
a |
b |
c |
d |
e |
f |
| 2×3×7 |
2×3×7×n2 |
2×3×7×m2 |
2×3×7×k2 |
2×3×7×t2 |
2×3×7×s2 |
2×3×7×r2 |
Ponieważ liczby te są parami różne, więc najmniejsze możliwe liczby
to:
2×3×7
2×3×7×22
2×3×7×32
2×3×7×42
2×3×7×52
2×3×7×62
2×3×7×72
Zatem największa z liczb będzie większa lub równa 2×3×7×72 = 42×49 = 2058, a więc będzie większa niż od 2007.
Joanna Jędrzejewska kl.IIa
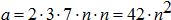
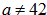 , więc w rozkładzie powinien wystąpić (dwukrotnie) jeszcze jeden
czynnik, który oznaczę literą n.
, więc w rozkładzie powinien wystąpić (dwukrotnie) jeszcze jeden
czynnik, który oznaczę literą n.