PREZENT WAKACYJNY 2006/7
DLA UCZNIÓW GIMNAZJUM
ZADANIE 9
Czy istnieje taka liczba naturalna k, że 5k jest piątą potęgą pewnej liczby całkowitej, 6k jest szóstą potęgą liczby całkowitej oraz 7k jest siódmą potęgą liczby całkowitej?
ROZWIĄZANIE
Istnieją takie liczby.
Najprostszy przykład to k = 0.
1.k=0
2.5k=0 i 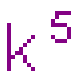 =0, więc 5k jest piątą potęgą liczby całkowitej.
=0, więc 5k jest piątą potęgą liczby całkowitej.
3.6k=0 i 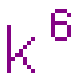 =0, więc 6k jest szóstą potęgą liczby całkowitej.
=0, więc 6k jest szóstą potęgą liczby całkowitej.
4.7k=0 i 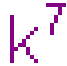 =0, więc 7k jest siódmą potęgą liczby całkowitej.
=0, więc 7k jest siódmą potęgą liczby całkowitej.
Inny przykład to k = 584×635×790
Ogólne rozwiązanie to k = 56×7×(5a+2)×65×7×(6b+1)×75×6×(7c+3) gdzie a, b, c to dowolne liczby naturalne.
Kinga Kępczyńska