LIGA ZADANIOWA UMK W TORUNIU 2007/2008
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM

Zadanie 10.

Dany jest trójkąt OAB, gdzie A=(-8,0), B=(0,-8) i O=(0,0). Niech A₁ będzie obrazem punktu A w symetrii osiowej względem prostej OB, B₁ obrazem punktu B w symetrii osiowej względem prostej OA i O₁ obrazem punktu O w symetrii osiowej względem prostej AB. Wyznacz pole trójkąta O₁A₁B₁.

Rozwiązanie

Musimy obliczyć pole trójkąta O₁A₁B₁.

1)Robimy kwadrat o punktach: O2=(-8,8), O3=(8,8) oraz O4=(8,-8)

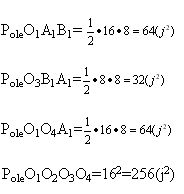
2)

3)Dodajemy pola: 64j²+32j²+64j²=160(j²)

4)Odejmujemy pola. PoleO₁A₁B₁=256-160=96j².

Odpowiedź. Pole trójkąta O₁A₁B₁ wynosi 96j².

Autorką jest Sandra Kisielewska z klasy IIa