LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 11
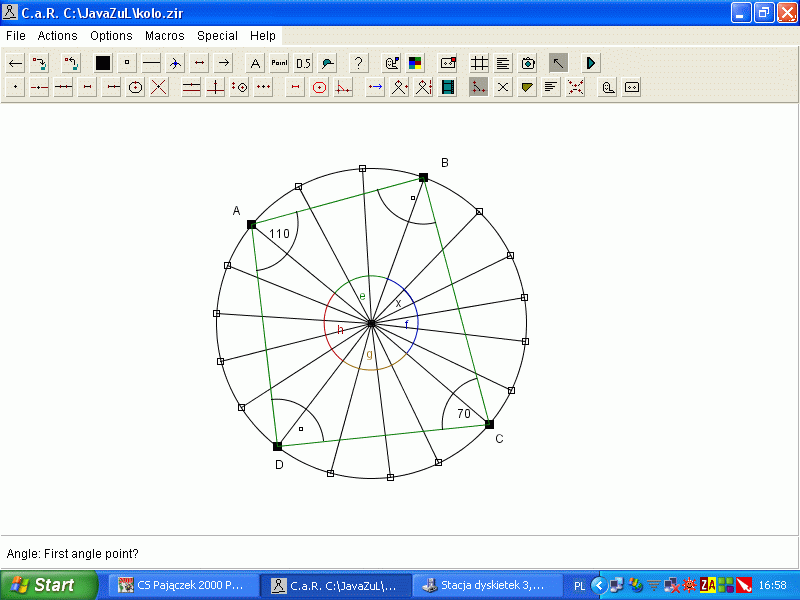
Na okręgu obrano kolejno punkty A, B, C, D, które podzieliły okrąg na częćści i stosunku 3:6:5:4. Oblicz miary kątów czworokąta ABCD.
Odp.: Kąt CBA ma 90°, kąt BAD ma 110°, kąt ADC ma 90°,a kąt DCB ma 70 °.
Rozwiązanie
Niech x oznacza 1/3 miary kąta środkowego opartego na łuku AB.Wtedy:
- Miara kąta środkowego opartego na łuku AB wynosi 3x.
- Miara kąta środkowego opartego na łuku BC wynosi 6x.
- Miara kąta środkowego opartego na łuku CD wynosi 5x.
- Miara kąta środkowego opartego na łuku DA wynosi 4x.
Kąty te w sumie tworzą kat pełny. Zatem
3x + 6x + 5x + 4x = 360°.
18x = 360°.
x = 20°.
Stąd:
- Miara kąta środkowego opartego na łuku AB wynosi e = 3x = 60°.
- Miara kąta środkowego opartego na łuku BC wynosi f = 6x = 120°.
- Miara kąta środkowego opartego na łuku CD wynosi g = 5x = 100°.
- Miara kąta środkowego opartego na łuku DA wynosi h = 4x = 80°.
Skorzystam z twierdzenia, że kąt wpisany jest dwa razy większy od kąta środkowego opartego na tym samym łuku.
- Kąt wpisany oparty na tym samym łuku co kąt CBA równa się 180°, więc kąt CBA jest równy 90°.
- Tak samo jest w przypadku kąta ADC(90°).
- Kąt wpisany oparty na tym samym łuku co kąt DCB równa się 140°, więc kąt DCB jest równy 70°.
- Ostatni kąt (BAD) jest równy 110°, ponieważ kąt wpisany oparty na tym samym łuku równa się 220°.
Odp.: Kąt CBA ma 90°, kąt BAD ma 110°, kąt ADC ma 90°,a kąt DCB ma 70 °.
Opracował Jan Kozakiewicz

