LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM

Zadanie 12

Wszystkie wierzchołki czworokąta ABCD leżą na okręgu, a przekątne czworokąta przecinają się w punkcie S różnym od środka okręgu. Ile stopni ma kąt ACD, jeśli miary kątów DAB, BSC, ABC są odpowiednio równe 80°, 50°, 110°?

Rozwiązanie zadania:

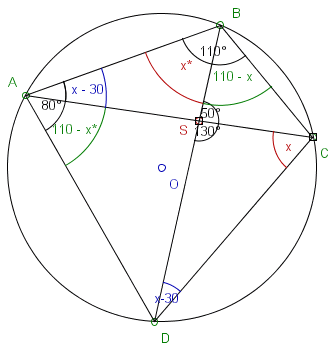
Powyższy rysunek to wizualne przedstawienie zadania.

Naszym zadaniem jest znalezienie mary kąta ACD, który oznaczymy jako "x"

Wiemy, że:

a) miara kąta ABD musi być równa "x*", gdyż kąt ABD leży na tym samym łuku co kąt "x", więc ma tą samą miarę;

b) miara kąta DBC jest równa: miara kąta ABC (110°) minus miara kąta ABD ("x"), więc miara kata DBC 110°-x

c) miara kąta CAD wynosi 110°-x, ponieważ kąt CAD opiera się na tym samym łuku co kąt DBC

d) W związku z powyższym punktem miara kąta CAB wynosi 30°-x, bo (110°-x)-80°=x-30°

e) Leżący na tym samym łuku co kąt CAB, kąt BDC również ma miarę x-30°

Dlatego aby obliczyć miarę kąta ACD rozwiązujemy następujące równanie:

(x-30°)+x+130°=180° (*)

2x-30°+130°=180°

2x+100°=180° /-100°

2x=80° /:2

x=40°

*(suma miar kątów w trójkącie, w tym przypadku to trójkąt DSC, wynosi 180°)

Diana Kryczko