LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 15
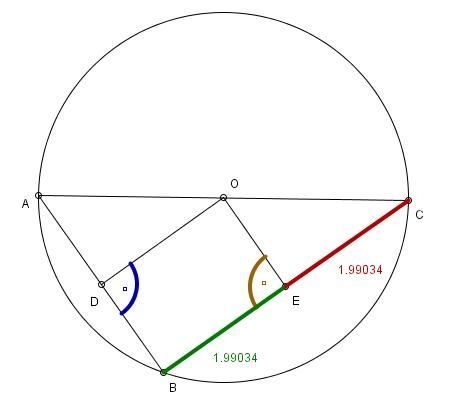
Na okręgu o środku O obrano trzy różne punkty A, B, C w ten sposób, że odcinek AC jest średnicą okręgu.
Następnie ze środka O poprowadzono odcinki OD i OE prostopadłe do cięciw AB i BC.
a) Jakim czworokątem jest czworokąt ODBE?
b) Uzasadnij, że AD="DB" oraz BE="EC."
Rozwiązanie
To zadanie, wbrew pozorom można rozwiązać bez rysunku. Ale w geometrii dużo prościej jest dojść do rozwiązania na rysunku.
Rysunki zamieszczam pod rozwiązaniami.
Rozwiązanie a)
Ponieważ odcinek OD leży prostopadle do odcinka AB tworzy się kąt prosty ODB.
Tak samo jest z odcinkiem OE prostopadłym do odcinka BC gdzie tworzy się kąt prosty OEB.
Kąt CBA tworzy kąt prosty, ponieważ jest oparty na średnicy.
Odpowiedź a)
Czworokąt ten to prostokąt ponieważ, jeśli jakiś czworokąt ma co najmniej 3 kąty proste to musi być prostokątem.
Rozwiązanie b)
Trójkąt ADO Jest trójkątem prostokątnym (kąt ADO jest kątem prostym). Jeżeli poprowadzimy promień OB to przedzielimy prostokąt
na dwa mniejsze trójkąty przystające. Trójkąt ADO i trójkąt OBD są przystające bo mają dwa boki tej samej długości i kąty między tymi bokami tej samej miary (cecha bkb przystawania trójkątów).
OB i OA są promieniami czyli są równe. OD jest bokiem wspólnym obu trójkątów. Między bokiem OB i OD jest kąt DOB, który jest równy kątem DOA. Jest równy ponieważ odcinek OD leży na
dwusiecznej kąta AOB.
A jeżeli trójkąty te są przystające to AD="BE." Podobnie jest z odcinkami BE i EC, gdzie trójkąty przystające to OBE i OEC.
Rysunki