| Zadanie 16 |
| W każdym z wielokątów na rysunkach poniżej oblicz sumę miar kątów, zaznaczonych łukami. Co zauważyłeś? |
Przykład a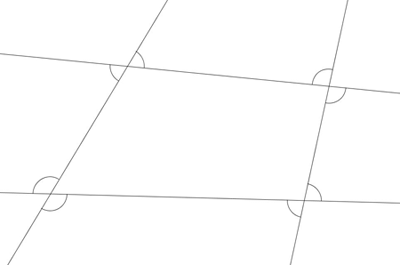 Przykład b 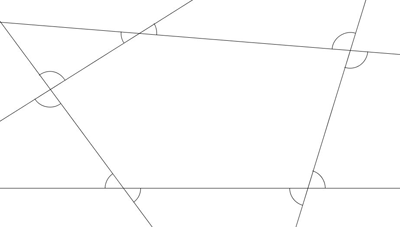 Przykład c 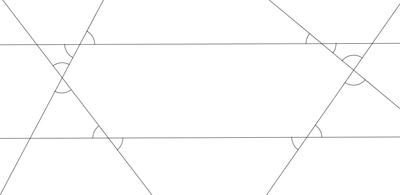 |
| Rozwiązanie przykładu a |
1. Na początku oznaczyłem wszystkie kąty tej samej miary jednym kolorem. 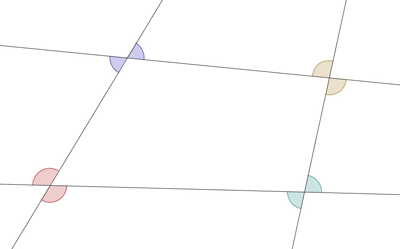 2. Mniej więcej na środku wyznaczyłem punkt P i połączyłem go ze wszystkimi wierzchołkami kątów. 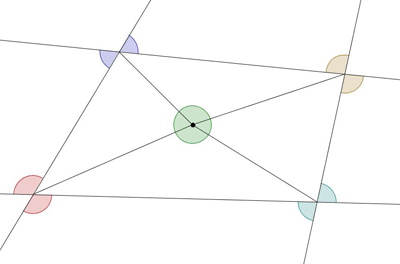 3. Zauważyłem, że kąty wewnętrzne czworokąta mają swoje lustrzane odbicia tzw. kąty wierzchołkowe. Na rysunku oznaczyłem je jednakowym kolorem. Zielone kółko symbolizuje kąt 360°. 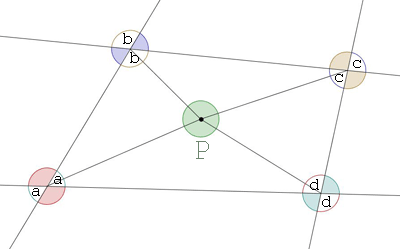 4. Następnie policzyłem kąty wewnętrzne czworokąta w następujący sposób: skoro utworzyły się 4 trójkąty, tak więc suma kątów wszystkich 4 trójkątów wynosi 720°. Jednak musiałem odjąć wszystkie 4 kąty przy wierzchołku punktu P. Tak więc suma wszystkich kątów wewnętrznych równa się: 720° - 360° czyli 360°. Kąty o tej samej literze są tej samej miary. Aby policzyć kąty oznaczone przykładzie a, trzeba odjąć od sumy wszystkich kątów kąty wewnętrzne, jak i ich zewnętrzne odpowiedniki, kąty wierzchołkowe. 360° x 4 = 1440° - suma wszystkich kątów. 1440° - 2 x 360° = 720° - suma oznaczonych kątów. |
| Odpowiedź: |
| Suma oznaczonych kątów równa jest 720°. |
| Rozwiązanie przykładu b |
| Zastosowałem to samo rozumowanie, co w punkcie a, tak więc suma kątów wewnętrznych w pięciokącie wynosi 540°, więc suma oznaczonych kątów jest równa 360° x 5 - 540° x 2 = 720°. |
| Odpowiedź: |
| Suma oznaczonych kątów równa jest 720°. |
| Rozwiązanie przykładu c |
| Po ponownym zastosowaniu tego samego rozumowania obliczyłem, że suma kątów wewnętrznych w sześciokącie równa jest 720°. Pomnożyłem to x 2 i aby dostać sumę oznaczonych kątów wykonałem działania: 360° x 6 - 720° x 2 = 720°. |
| Odpowiedź: |
| Suma oznaczonych kątów równa jest 720°. |
| Wnioski: |
|
Z powyższych przykładów można wysnuć wniosek, że suma oznaczonych kątów w dowolnym wielokącie zawsze jest równa jest 720°, gdyż:
w n-kącie, suma kątów wewnetrznych wynosi (n-2)×180°, więc suma kątów zewnętrznych jest równa: n×360° - 2×(n -2)×180° = n×360° - (n - 2)×360° = 2×360° = 720°. Alan Mamrzyński |