PREZENT WAKACYJNY 2006/7
DLA UCZNIÓW GIMNAZJUM

Zadanie 17

W trójkącie ABC poprowadzono środkową AM. Czy promień okręgu wpisanego w trójkąt ABM może być dwa razy większy od promienia okręgu wpisanego w trójkąt ACM?

Rozwiązanie:

Przypuśćmy, że to jest możliwe. Przyjmijmy oznaczenia jak na rysunku gdzie s=środkowa trójkąta ABC. Wtedy: 
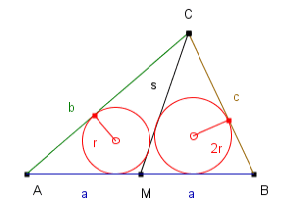
Pole (BMC)=Pole (AMC)
1×2r(a+s+c)=1 r(a+s+b)
2a+2s+2c=a+s+b/-a-s-2c
a+s=b-2c
Z nierówności trójkąta (dla trójkąta AMC): 
a+s>b
b-2c>b
-2c>0
2c<0
c<0
A to jest niemożliwe, żeby długość boku była ujemna.

Odp.: Promień okręgu wpisanego w trójkąt ABM nie może być dwa razy większy od promienia okręgu wpisanego w trójkąt ACM

Jakub Misiaszek kl.IIa