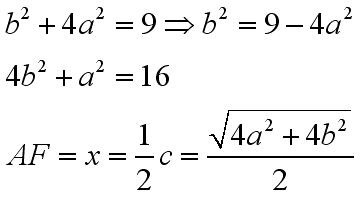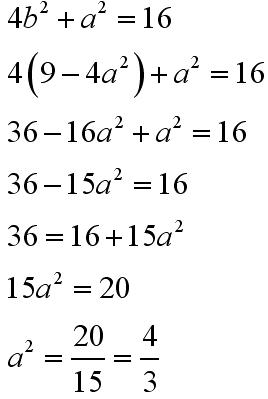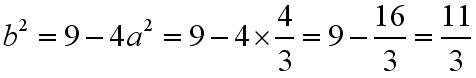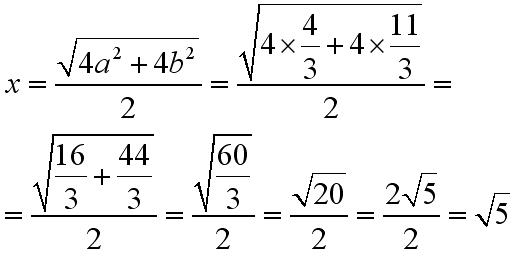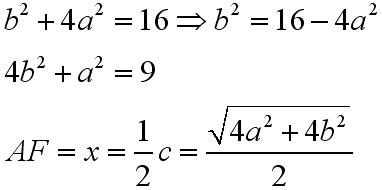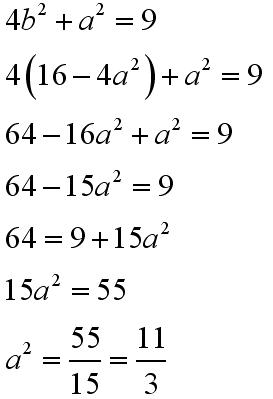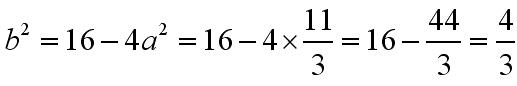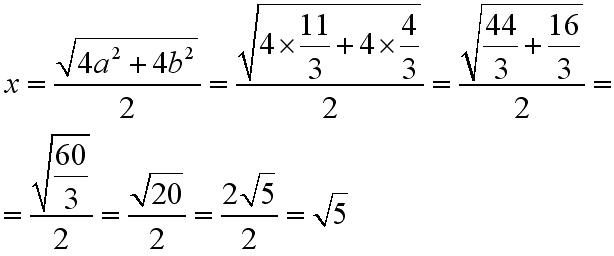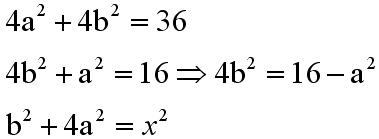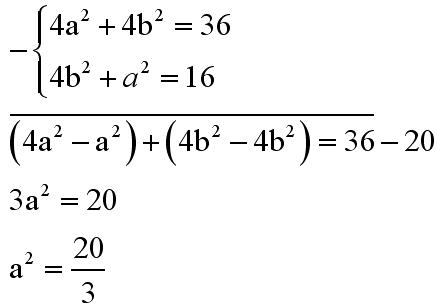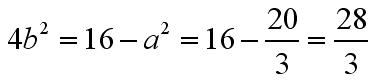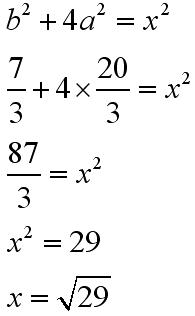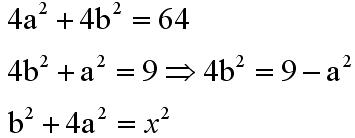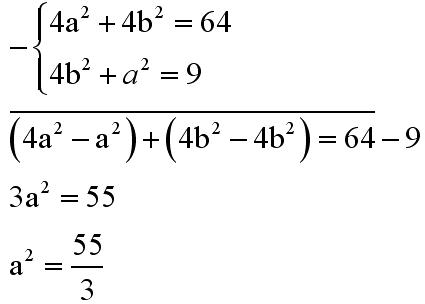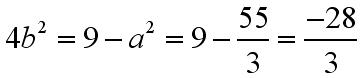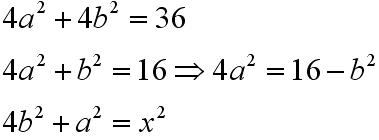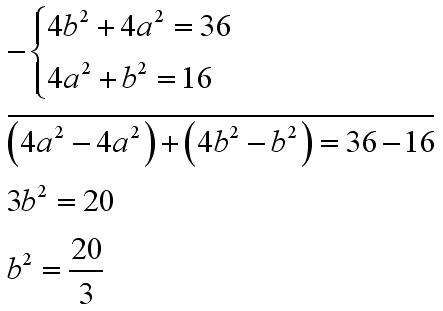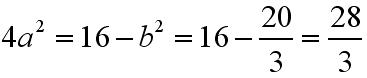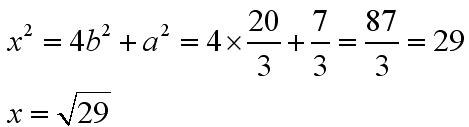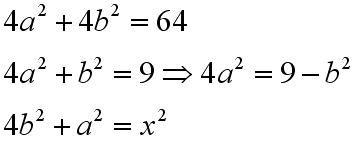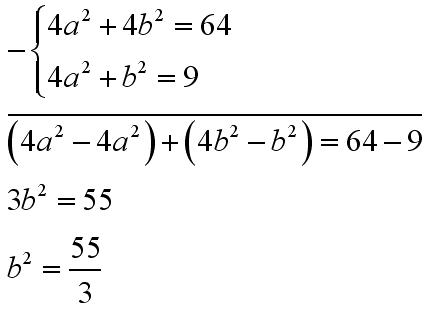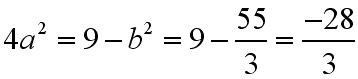PREZENT WAKACYJNY 2006/7
DLA UCZNIÓW GIMNAZJUM

Zadanie 23

W trójkącie prostokątnym dwie środkowe mają długości 3 i 4. Jaką długość ma trzecia środkowa?

Rozwiązanie:

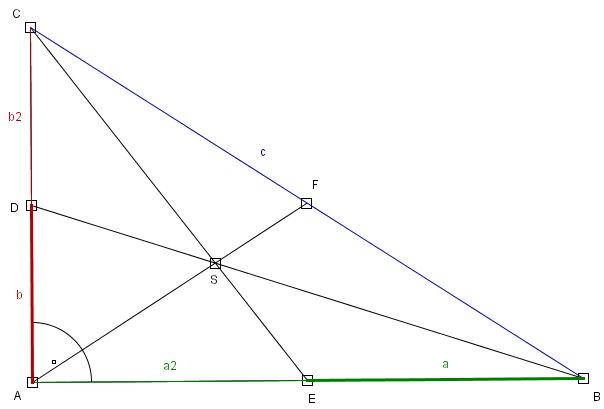
a=a2 - połowa odcinka AB

b=b2 - połowa odcinka AC

c - odcinek BC

W zadaniu tym należ rozważyć kilka przypadków, gdyż nie wiemy która środkowa jest naszą niewiadomą.

PRZYPADEK 1 gdy niewiadomą jest dlugość środkowej FA

FA=x=1/2c (promień okręgu opisanego)

1)CE=4 i BD=3

Z twierdzenia Pitagorasa wiemy że:

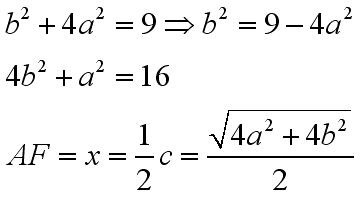
Do drugiego równania możemy podstawić b podniesione do kwadratu wyznaczone z pierwszego równania:

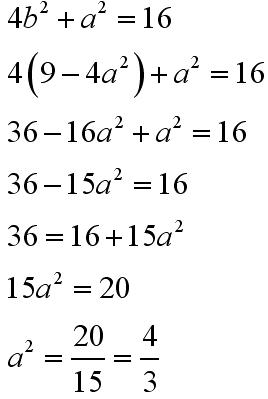
Po otrzymaniu a do kwadratu można wyznaczyć b:

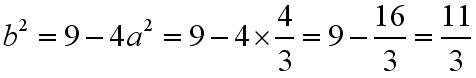
Znając a i b podniesione do potęgi drugiej można obliczyć x:

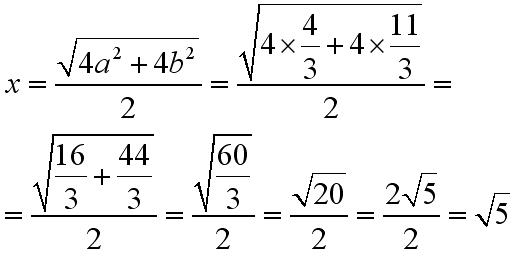
2)CE=3 i BD=4

Z twierdzenia Pitagorasa wiemy że:

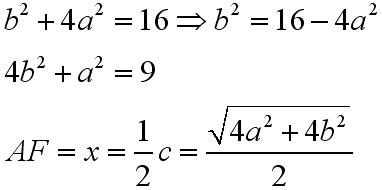
Podstawiamy za b do kwadratu:

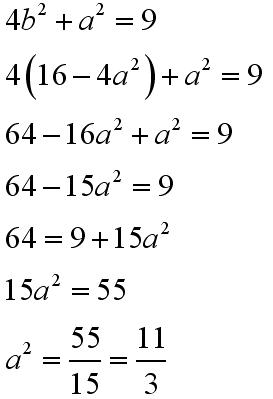
Wyznaczamy b:

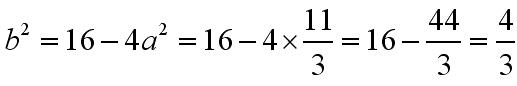
Liczymy x:

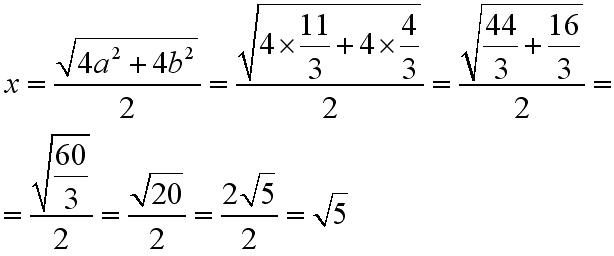
PRZYPADEK 2 gdy niewiadomą jest dlugość środkowej DB

DB=x

1)AF=3 i CE=4

c=2*AF=2*3=6

Z twierdzenia Pitagorasa:

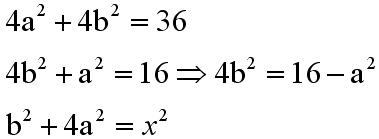
Rozwiązujemy układ równań:

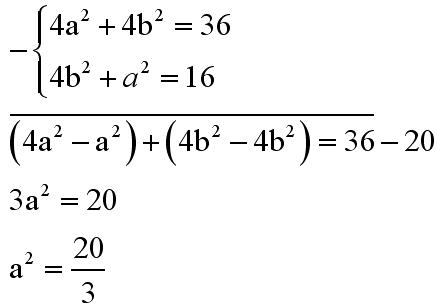
Wyznaczamy b:

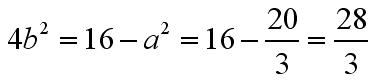
Mamy już b i a, możemy wyznaczyć więc x:

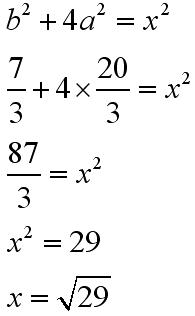
2)AF=4 i CE=3

c=2*AF=2*4=8

Z twierdzenia Pitagorasa:

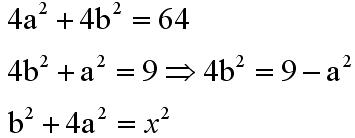
Rozwiązujemy układ równań:

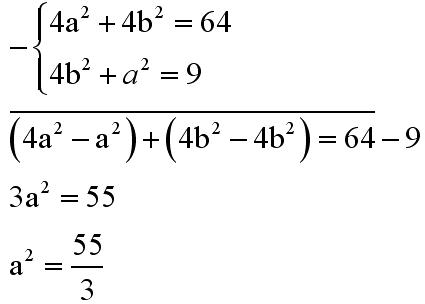
Wyznaczamy b:

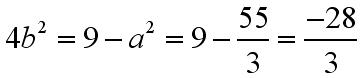
Sprzeczność

PRZYPADEK 3 gdy niewiadomą jest dlugość środkowej CE

CE=x

1)AF=3 i DB=4

c=2*AF=2*3=6

Z twierdzenia Pitagorasa:

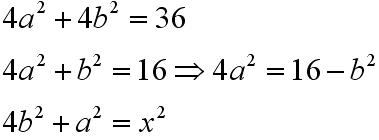
Rozwiązujemy układ równań:

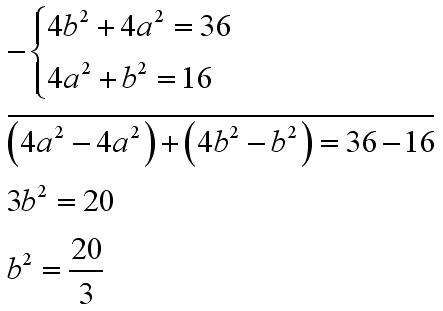
Wyznaczamy b:

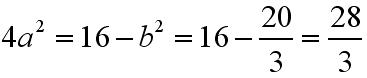
Mamy już b i a, możemy wyznaczyć więc x:

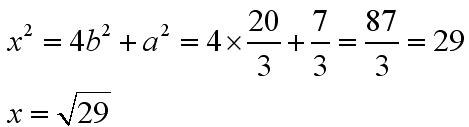
2)AF=4 i DB=3

c=2*AF=2*4=8

Z twierdzenia Pitagorasa:

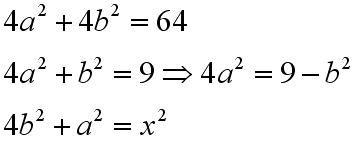
Rozwiązujemy układ równań:

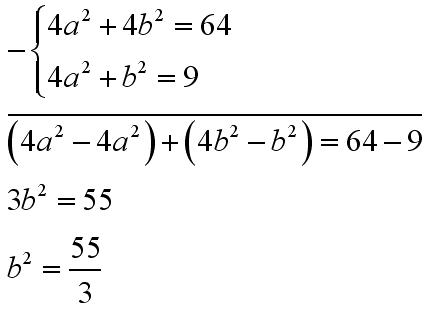
Wyznaczamy b:

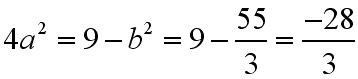
Sprzeczność

Odpowiedź:Trzecia środkowa ma długość pierwiastka z 5 lub pierwiastka z 29.

Opracował: Filip Solarczyk