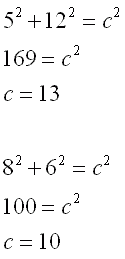Zadanie 24 - Liga wakacyjna

PREZENT WAKACYJNY 2006/7
DLA UCZNIÓW GIMNAZJUM

Zadanie 24

Wyznaczyć wszystkie trójkąty prostokątne, których długości boków są liczbami naturalnymi i pole trójkąta jest równe jego obwodowi.

Rozwiązanie

Jeśli pole równa się obwodowi i jest to trójkąt prostokątny, to mamy sytuację:

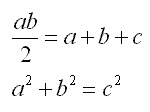
ab / 2 = a + b + c; a^2 + b^2 = c^2

gdzie a i b to przyprostokątne, a c to przeciwprostokątna.
Przekształcimy teraz pierwsze równanie.

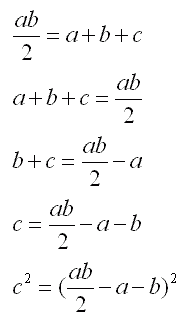
c^2=(ab / 2 - a - b)^2

Po przekształceniu możemy stwierdzić, że

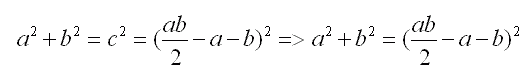
a^2 + b^2 = (ab/2 - a- b)^2

Sprowadźmy je do najprostszej postaci.

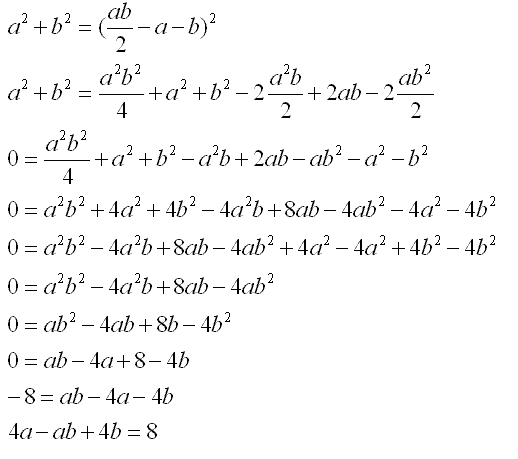
ab - 4a - 4b = -8 /+16

ab - 4a - 4b + 16 = 8

a(b - 4) - 4(b - 4) = 8

(a - 4)(b - 4) = 8

Liczby a i b są naturalne więc mamy następujące mozliwości:

a - 4 = 1 i b - 4 = 8, skąd a = 5 i b = 12.
a - 4 = 2 i b - 4 = 4, skąd a = 6 i b = 8.
a - 4 = 4 i b - 4 = 2, skąd a = 8 i b = 6.
a - 4 = 8 i b - 4 = 1, skąd a = 12 i b = 5.
a - 4 = -1 i b - 4 = -8, skąd a = 3 i b = -4.
Odrzucamy tę możliwość bo -4 nie jest liczbą naturalną.
a - 4 = -2 i b - 4 = -4, skąd a = 2 i b = 0.
Odrzucamy tę możliwość bo długość boku b musi być liczba dodatnią.
a - 4 = -4 i b - 4 = -2, skąd a = 0 i b = 2.
Odrzucamy tę możliwość bo długość boku a musi być liczba dodatnią.
a - 4 = -8 i b - 4 = -1, skąd a = -4 i b = 3.
Odrzucamy tę możliwość bo -4 nie jest liczbą naturalną.

Ostatecznie mamy cztery rozwiązania: (a=5, b= 12),(a=6, b=8),(a=8, b=6), (a=12, b=5). Obliczmy teraz c dla tych trójkątów.

ODPOWIEDŹ: Takie trójkąty to (a=6, b=8, c=10),(a=8, b=6, c=10),(a=12, b=5, c=13),(a=5, b=12, c=13)

Autor: Jakub Szmigiel, Gimnazjum 11 w Toruniu