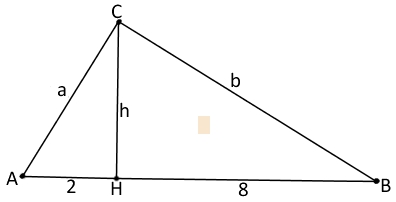
|AH| = 2cm
|HB| = 8 cm
|AB| = 10 cm
a2 + b2 = 102
82 + h2 = b2
22 + h2 = a2
a2 + b2 = 100
64 + h2 = b2 /-64
4 + h2 = a2 /-4
h2 = b2 - 64
h2 = a2 - 4
b2 - 64 = a2 - 4 /+64
b2 = a2 + 60
b2 = 100 - a2
b2 = a2 +60
100 - a2 = a2 + 60 /-60
40 - a2 = a2 /+a2
40 = 2a2 /:2
20 = a2 / ![]()
![]() = a
= a
2![]() = a
= a
a2 + b2 = 102 P = a * b : 2 Obw. = a + b + 10
(2![]() )2 + b2 = 102
)2 + b2 = 102
20 + b2 = 100 /-20
b2 = 80 /![]()
b2 = ![]()
b = 4![]()
P = 2![]() * 4
* 4![]() : 2
: 2
P = 20
Obw. = 2![]() * 4
* 4![]() + 10
+ 10
Obw. = 6![]() + 10
+ 10