LIGA ZADANIOWA UMK W TORUNIU 2002/2003
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 27
Współrzędne wierzchołków trójkąta ABC wynoszą:
A=(2,-1), B=(-3,2), C=(-3,-3). Oblicz pole trójkąta ABC.
Rozwiązanie
Odcinek BC jest równoległy do osi y, ponieważ pierwsze
współrzędne punktów B i C są równe.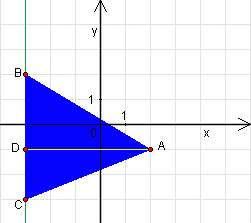
Niech odcinek równoległy do osi x wychodzący z punktu A przecina
odcinek BC w punkcie D. Ponieważ odcinek AD jest równoległy do osi x, a odcinek BC jest równoległy do osi y, więc odcinek AD
jest prostopadły do BC, czyli jest on wysokością w trójkącie ABC.
Długość odcinka AD wynosi 5, gdyż punkt A jest oddalony od osi
y o 2 jednostki(współrzędna x punktu A równa się 2), zaś D jest oddalony od osi y o 3 jednostki(współrzędna x punktu D równa się -3,gdyż
punkt ten leży na prostej równoległej do osi y o współrzędnej -3).
Długość odcinka BC wynosi 5, gdyż punkt B jest oddalony od osi
x o 2 jednostki(współrzędna y punktu B równa się 2), zaś C jest oddalony od osi x o 3 jednostki (współrzędna y punktu C równa się -3).
Pole trójkąta ABC wynosi ½×AD×BC, czyli ½×5×5=12.5
Odpowiedź
Pole trójkąta ABC jest równe 12.5.
Iwona Lis

