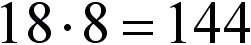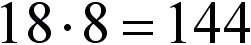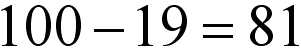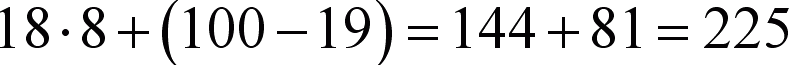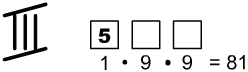Ile istnieje trzycyfrowych liczb przy zapisie których użyto tylko raz cyfry 5?
Rozwiązanie:
I sposób:
Najpierw wypisuję kolumnami liczby od 100 do 199, 200-299, 300-399, 400-499, 600-699, 700-799, 800-899, 900-999, w których tylko raz wystąpiła cyfra "5".
Są to liczby:
| 105 |
205 |
305 |
405 |
605 |
705 |
805 |
905 |
| 115 |
215 |
315 |
415 |
615 |
715 |
815 |
915 |
| 125 |
225 |
325 |
425 |
625 |
725 |
825 |
925 |
| 135 |
235 |
335 |
435 |
635 |
735 |
835 |
935 |
| 145 |
245 |
345 |
445 |
645 |
745 |
845 |
945 |
| 150 |
250 |
350 |
450 |
650 |
750 |
850 |
950 |
| 151 |
251 |
351 |
451 |
651 |
751 |
851 |
951 |
| 152 |
252 |
352 |
452 |
652 |
752 |
852 |
952 |
| 153 |
253 |
353 |
453 |
653 |
753 |
853 |
953 |
| 154 |
254 |
354 |
454 |
654 |
754 |
854 |
954 |
| 156 |
256 |
356 |
456 |
656 |
756 |
856 |
956 |
| 157 |
257 |
357 |
457 |
657 |
757 |
857 |
957 |
| 158 |
258 |
358 |
458 |
658 |
758 |
858 |
958 |
| 159 |
259 |
359 |
459 |
659 |
759 |
859 |
959 |
| 165 |
265 |
365 |
465 |
665 |
765 |
865 |
965 |
| 175 |
275 |
375 |
475 |
675 |
775 |
875 |
975 |
| 185 |
285 |
385 |
485 |
685 |
785 |
885 |
985 |
| 195 |
295 |
395 |
495 |
695 |
795 |
895 |
995 |
Tych liczb jest:
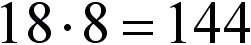
A teraz wypisuje liczby od 500 do 599, które maja co najmniej dwie cyfry"5":
| 505 |
| 515 |
| 525 |
| 535 |
| 545 |
| 550~~~~~~~~ |
551 |
552 |
553 |
554 |
555 |
556 |
557 |
558 |
559 |
| 565 |
| 575 |
| 585 |
| 595 |
Tych liczb jest:
10+9="19
Teraz od 100 liczb (bo od 500-599, jest 100 liczb) odejmuje liczby przy których zapisie użyłam więcej niż jedna cyfrę "5":
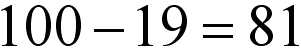
Podsumowując:
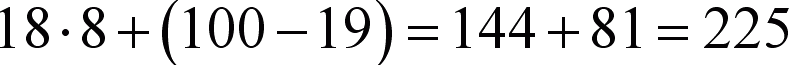
II sposób:
Przedstawiam wszystko na trzech "drzewach":
- Pierwsze drzewko pokazuje ile jest liczb, które mają piątkę na miejscu jedności (J).
Jeśli cyfra 5 jest w miejscu jedności jest, to miejsce dziesiątek można uzupełnić na 9 sposobów (cyframi 0, 1, 2, ,3 ,4 , 6 ,7 , 8) i miejsce setek można uzupełnić na 8 sposobów (cyframi 1, 2, ,3 ,4 , 6 ,7 , 8).
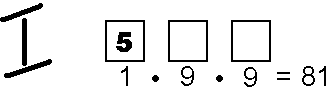
- Drugie drzewko pokazuje ile jest liczb, które mają piątkę na miejscu dziesiątek (D).
Jeśli cyfra 5 jest w miejscu dziesiątek jest, to miejsce jedności można uzupełnić na 9 sposobów (cyframi 0, 1, 2, ,3 ,4 , 6 ,7 , 8) i miejsce setek można uzupełnić na 8 sposobów (cyframi 1, 2, ,3 ,4 , 6 ,7 , 8).
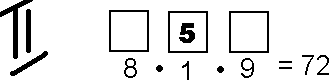
- Trzecie drzewko pokazuje ile jest liczb, które mają piątkę na miejscu setek (S).
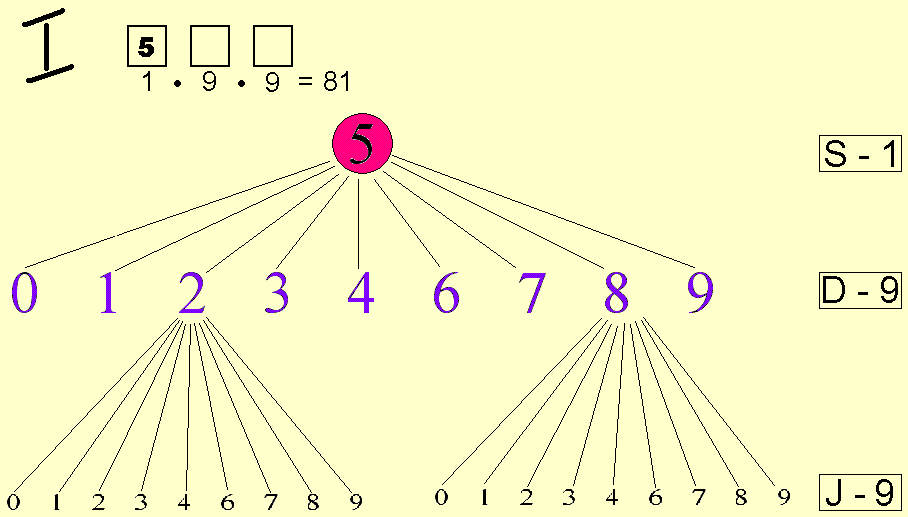
Jeśli cyfra 5 jest w miejscu setek jest, to miejsce jedności można uzupełnić na 9 sposobów (cyframi 0, 1, 2, ,3 ,4 , 6 ,7 , 8) i miejsce dziesiątek można uzupełnić na 9 sposobów (cyframi 0, 1, 2, ,3 ,4 , 6 ,7 , 8).
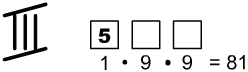
Pierwsze drzewko
Drugie drzewko
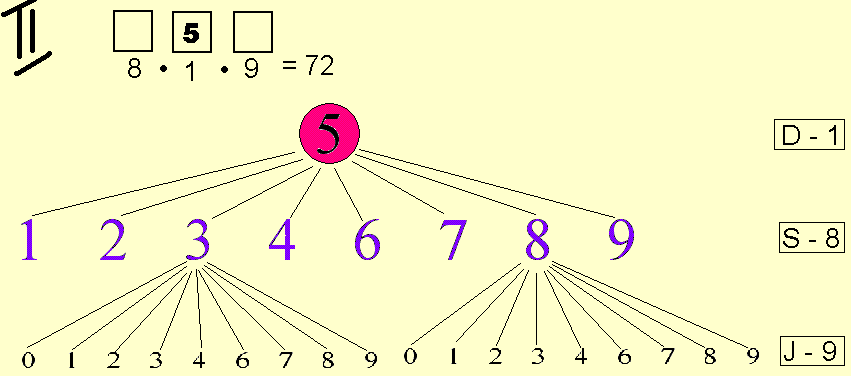
Trzecie drzewko
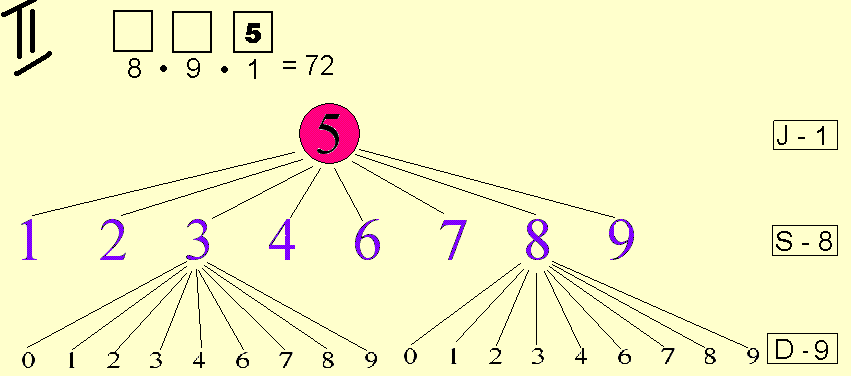
Razem możliwości:
81+72+72="225" liczb
Odpowiedź:
Liczb przy zapisie których użyto tylko raz cyfry 5 jest 225.
Monika CHWIAŁKOWSKA