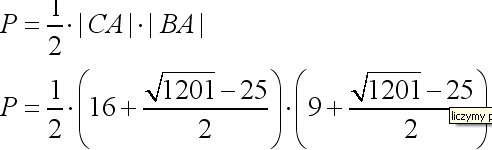LIGA ZADANIOWA UMK W TORUNIU 2007/2008
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM

Zadanie 18
Punkt styczności okręgu wpisanego w trójkąt prostokątny z przeciwprostokątną dzieli tę przeciwprostokątną na dwa odcinki długości 16 i 9. Obliczyć pole i obwód tego trójkąta.

Rozwiązanie:
Zacznijmy od narysowania rysunku pomocniczego.

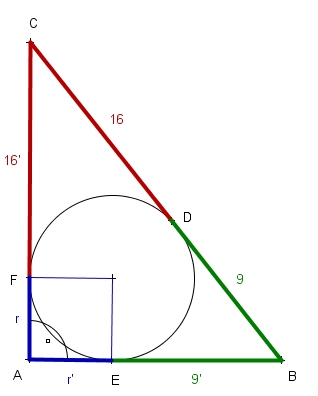
RYSUNEK POMOCNICZY


Dlaczego na rysunku są dwie pary odcinków o tej samej długości? Otóż z twierdzenia o odcinkach stycznych:

Dla dowolnego okręgu i dowolnego punktu leżącego na zewnątrz tego okręgu,
jeżeli przez ten punkt poprowadzimy proste styczne do danego okręgu,
to odcinki łączące ten punkt z punktami stycznosci są równej długości.

Tak więc |CF|=|CD| oraz |BD|=|BE|. Poza tym |AE|=|FA|, ponieważ są to odcinki o takich samych miarach jak promień koła wpisanego w trójkąt ABC (a promień w kole ma tylko jedną długość). Teraz wykorzystajmy to, iż bok AC=CF+r oraz BA=|BE+r stosując przy okazji twierdzenie Pitagorasa.

(r + 9)2 + (r + 16)2 = 252

r2 + 18r + 81 + r2 +32r + 256 = 625

2r2 + 50r = 268

r2 + 25r = 134

           r2 + 2×12,5r = 134       / + (12,5)2

(r + 12,5)2 = 1201/4

r + 12,5 = pierwiastek(1201)/2

r = pierwiastek(1201)/2 - 12,5

Teraz policzenie obwodu będzie wyjątkowo proste.

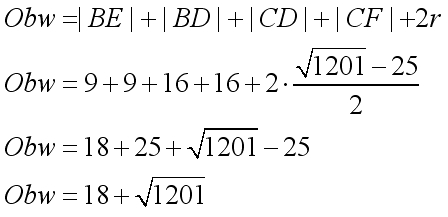
liczenie obwodu trójkąta ABC


Następnie policzmy pole trójkąta ABC.

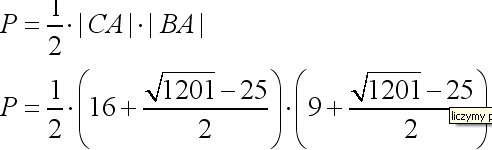
liczymy pole trójąta ABC

Rafał Mossakowski