LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM
Zadanie 17
W trójkącie prostokątnym przyprostokątne mają długości
6 cm i 8 cm. Oblicz długości odcinków, na które dzieli
przeciwprostokątną wysokość opuszczona z wierzchołka kąta
prostego.
Rysunek:
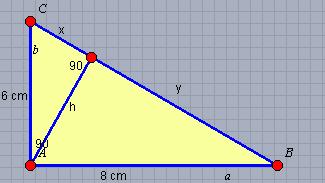
Obliczamy pole całego trójkąta za pomocą wzoru:
P="1/2.a.b
gdzie:
a = 8 cm -jest podstawą
b = 6 cm -jest wysokością
P="1/2.8.6
P="24" (cm2)
Patrząc z innej perspektywy, pole możemy obliczyć w ten sposób:
Z twierdzenia Pitagorasa
(x+y)2=82+62
(x+y)2=100
x+y="10
P="1/2.(x+y).h
P="1/2.10.h
24="5.h
h="24:5
h="4,8" (cm2)
Z twierdzenia Pitagorasa:
x2+h2=b2
x2+4,82=62
x2+23,04="36
x2=36-23,04
x2=12,96
x="3,6
y="(x+y)-x
y="10-3.6
y="6,4

