LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA GIMNAZJUM

ZADANIE
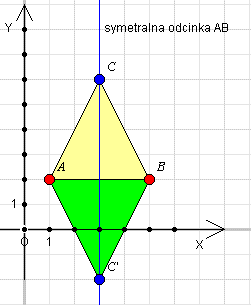
Odcinek o końcach A="(1,2)," B="(5,2)" jest podstawą trójkąta równoramiennego ABC o polu 8.  Wyznaczyć punkt C.
Rozwiązanie
Punkt C musi być równo oddalony od punktów A i B, więc leży na symetralnej odcinka AB. Wiemy też, że jeżeli wyznaczymy punkt C, to odcinek poprowadzony od punktu C pod kątem 90o do AB będzie wysokością trójkata ABC. Pole P trójkąta ABC wyraża się wzorem P="1/2" a . h gdzie a="|AB|=4 h = odległość punktu C od AB. P="1/2.4.h Ponieważ P="8," więc h="4. Aby wysokość wynosiła 4 punkt C musi być oddalony od podstawy o 4 jednostki. Odpowiedź: C="(3,6)" lub C="(3,-2)

Mary