Tytuł

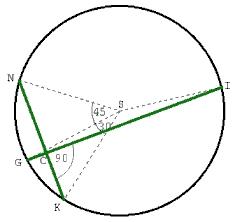
LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA GIMNAZJUM

ZADANIE 5
Teść zadania Dwie cięciwy przecinają się pod kątem prostym i dzielą okrąg na cztery łuki. Kąty środkowe oparte na najkrótszych łukach są równe 30^o i 45^o. Wyznacz kąty środkowe oparte na pozostałych łukach.

Rozwiązanie:

Dla ułatwienia rozwiązania zadania, łączymy odcinkiem punkty K i I, G i N, N i I.
Kąty : GIK i GNK są kątami wpisanymi opartymi na tym samym łuku co kąt środkowy GSK, więc ich miary są równe 15^o.
Trójkąt GSN jest trójkątem równoramiennym, więc kąty przy jego podstawie są sobie równe. Z tego wynika, że kąt NGS = (180^o-45^o):2=67,5^o, a kąt KNS=67,5^o-15^o=52,5^o.

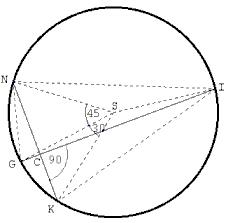
Teraz zajmę się trójkątem INC. Kąt GIN jest kątem wpisanym opartym na tym samym łuku co kąt środkowy GSN, więc kąt GIN=(1/2)*45^o=22,5^o. Kąt KNI=180^o-(90^o+22,5^o)=67,5^o. Aby obliczyć kąt SNI musimy od 67,5^o odjąć 52,5^oco daje wynik 15^o.
Kąt SNI =15^o,trójkąt NSI jest trójkątem równoramiennym, więc kąt NSI =180^o-(2*15^o)=150^o
Został nam teraz tylko jeden kąt do obliczenia, kąt KSI, obliczymy go tak:360^o-(45^o+30^o+150^o)=130^o
Kąt KSI =130^o

ZADANIE 5

Teść zadania

Rozwiązanie:

Kinga Czyżewska