LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA SZKÓŁ PODSTAWOWYCH

ZADANIE 5

Przypomnienie treści zadania:
Średnice okręgu o długości 6cm przecinają się pod kątem prostym. Ze środka łuku DA leżącego w punkcie E poprowadzono prostopadłe do odpowiednich średnic DB oraz AC i otrzymano na nich punkty G oraz F. Znajdź długość odcinka GF.
 Rozwiązanie:
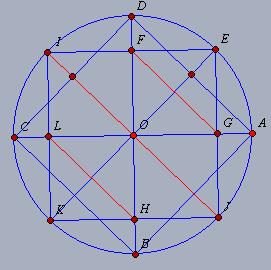
Rozmiar: 14386 bajtów
Dwie średnice AC i DB, przecinające się pod kątem prostym. W ten sposób dzielą okrąg na 4 części.
Gdy połączymy odc. punkty: FE , EG, OF i OG , otrzymamy kwadrat, którego przekątną jest szukana tego zadania czyli odc. FG.
Następnie rysujemy taka samą sytuacje , na każdej części okręgu. Jak przedstawia to rysunek obok. Wszystkie 4 kwadraty tworzą jeden duży kwadrat JEIK, którego przekątna jest średnica tego okręgu. Ta średnica składa się z dwóch przekątnych małych kwadratów.
Dlatego też odc. FG =0,5 odc. IJ ,
więc odc. FG = 3cm

Odp.Miara odcinka|FG|=3cm.

Kinga Czyżewska kl. Ia