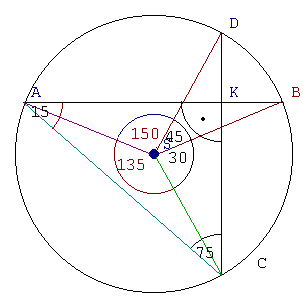
1) Najpierw na podstawie treści zadania sporządzamy rysunek (dorysowujemy cięciwę AC) i oznaczamy go.
2) Zauważamy, że kąt wpisany CAB jest oparty na tym samym łuku, co kąt środkowy CSB. Wiemy, że kąt CSB ma miarę 30^o, więc kąt CAB ma miarę 15^o (30:2=15^o).
3) Następnie obliczmy miarę wszystkich kątów w trójkącie AKC. Wiemy, że cięciwy przecinają się pod kątem prostym więc kąt CKA ma 90^o. Kąt CAK jak już wiemy ma 15^o. 90+15=105. Suma miar kątów w trójkącie powinna być równa 180^o. Żeby obliczyć miarę kąta KCA musimy od 180-105^o. Wychodzi 75^o. (180-105=75^o).
4) Kąt wpisany KCA (75^o) znajduje się na tym samym łuku co kąt środkowy DSA. W takim razie kąt DSA ma 150^o (2x75=150^o)
5) Do obliczenia pozostał nam już tylko jeden kąt CSA. Dodajmy miary wszystkich obliczonych kątów do siebie: 15+30+150=225^o . Wiemy, że kąt pełny ma 360^o, więc 360-225=135^o . Kąt CSA ma 135^o!!!