LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA PRZYGOTOWAWCZE DO ETAPU IV
DLA GIMNAZJUM
ZADANIE 8
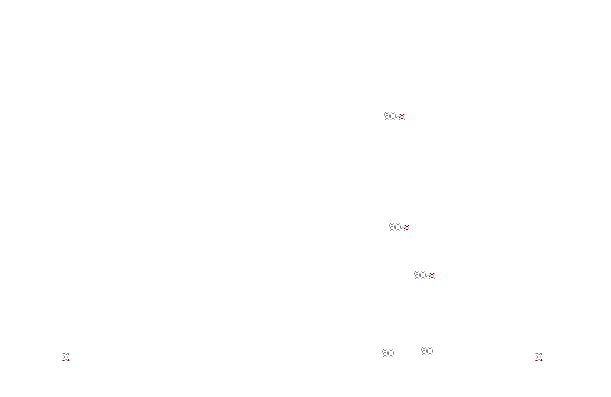
Jedno z ramion trójkata równoramiennego ABC przecięto prostą prostopadłą do podstawy AB. Prosta ta na przedłużeniu boku AC wyznaczyła punkt K, na ramieniu BC punkt L, a na podstawie AB punkt M. Uzasadnij, że trójkąt KLC jest równoramienny.
| 1) | Niech kąt CAB ma x stopni. |
| 2) | Ponieważ trójkąt ABC jest równoramienny więc kąt ABC ma też x stopni. |
| 3) | Ponieważ trójkąt ANK jest prostokątny, więc kąt CKL ma 90-x stopni. |
| 4) | Ponieważ trójkąt BNL jest prostokątny, więc kąt NLB ma 90-x stopni. |
| 5) | Ponieważ kąty BLN i KLC są wierzchołkowe, więc CLK ma 90-x stopni. |
| 6) | Kąty CLK i CKL mają oba po 90-x stopni, więc trójkąt KLC jest równoramienny. |
 |