Rozwiązanie
x2+2001= y2 gdzie xÎN i yÎN
x2-y2= -2001
Korzystając ze wzoru skróconego mnożenia....
(x+y)*(x-y)= -2001
(y-x)*(y+x)= 2001
(y - x)*(y + x)= 1*3*23*29
(y - x) < (y + x)
(y - x)*(y + x)= 1*2001= 3*667= 23*87*29*69
Czyli otrzymujemy następujące możliwości....
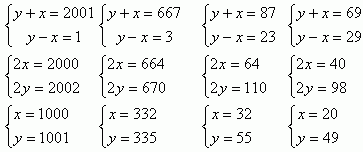
Autor rozwiązania: Paweł Kocyk