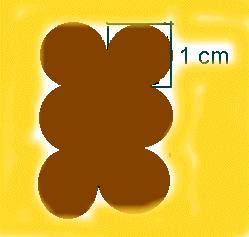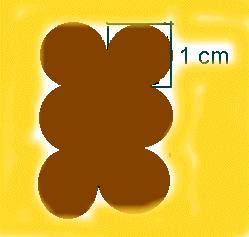Pole siatki "katarzynki" wynosi: 6*1 cm², czyli 6 cm².
Pole okręgów wszystkich wynosi 6* Pr²
r²=0,5²=0,25
Z tego wynika, że:
pole jednego okręgu wynosi:=P*0,25
3,14*0,25="0,785"
Stąd wnioskuję, że pole w jednym kwadracie, poza okręgiem pole wynosi: 1 cm²-0,785 cm², co się równa 0,215 cm².Takie pole przedstawione jest kolorem zielonym (w wewnątrz kwadratu) na rysunku poniżej.


Figura ta jest podzielona na 4 jednakowe części. Jedna taka część ma powierzchnię 0,215:4= 0,5375 cm².
Aby figura ta (duży prostokąt 3x2) miała kształt "katarzynki", należy odjąć od niej 16 takich fragmentów o polu 0,5375 cm².
Stąd ostateczne pole "katarzynki" wynosi: 6 cm²- (16*0,5375)cm²= 6 cm²- 0,86 cm²= 5,14 cm².