LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA SZKÓŁ PODSTAWOWYCH

ZADANIE 13

Na oceanie jest 5 wysepek A, B, C, D, E. Niektóre odległości między nimi są znane, mianowicie |AB|=|BC|=|AC|=3km, |CD|=|DE|=|EC|=8km, |BD|=11km. Oblicz odległość między wysepkami A i E.

ROZWIĄZANIE

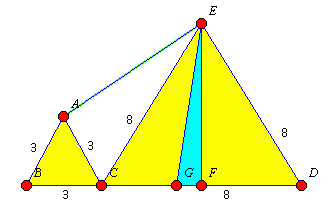
Odcinki |BC| i |CD| leżą na tej samej prostej, bo |BC| + |CD| = 11 ; a |BD| = 11. Z tego wynika, że punkt C leży na odcinku |BD|. Trójkąty |ABC| i |CDE| są równoboczne. Trójkąt |AEC| ma wymiary x, 8, 3 km.

Spójrzmy na rysunek u góry. Odcinek |EF| to wysokość - h. Obliczmy ją:

h²+4²=8²
h²+16=64
h²=48

Spójrzmy na niebieski trójkąt |EFG|. |FG|=1km. Obliczmy długość odcinka |EG| = z.

1²+h²=z²
1+48=z²
49=z²
z=7
Odcinek |EG|=7km.

Zwróćmy uwagę, że trójkąt |CGE| przystaje do trójkąta |AEC|, a odcinek |AE| jest przystający do |EG|