Treść zadania: Cięciwa dzieli okrąg na dwa łuki stosunku
3:7. Wyznaczyć kąt jaki tworzy ta cięciwa ze styczną poprowadzoną do okręgu w
jednym z końców tej cięciwy. Rozwiązanie: Wiemy, że okrąg ma w
środku kąt 360o, a więc każda z dziesięciu części, na które podzielimy okrąg
będzie tworzyła kąt o wartości 36o. Z tego wiemy, że trzy takie części
tworzyć będą kąt 108o. Można stworzyć trójkąt równoramienny AOB i wyliczyć miarę b kąta przy podstawie tego trójkąta. Wiemy, że suma kątów w trójkącie jest równa 180o,
więc układamy równanie: 180o-108o=2b
72o=2b /:2 36o=b
Wiemy, że styczna, z promieniem tworzy kąt 90o.
Po odjęciu 36o od 90o otrzymamy miarę a szukanego kąta równą
54o.
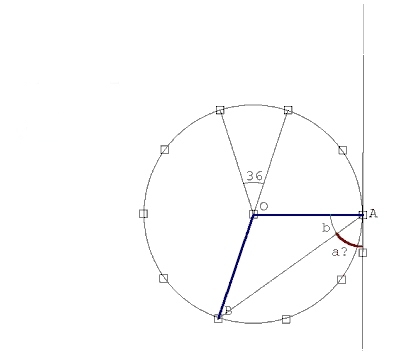
Całą tę sytuację przedstawia zamieszczony rysunek:
Jeżeli jesteś "pechowym" posiadaczem programu Car, to możesz ściągnąć tę konstrukcję: Download
