LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA GIMNAZJUM

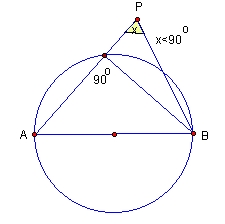
Gdyby istniał taki punkt P wewnątrz czworokąta, którego nie dosięgnęło by żadne z półkol to każdy z kątów x, y, z, t (rysunek poniżej) miałby mniej niż 90 stopni, tak jak to widać na przykładzie kąta x ( rysunek obok).
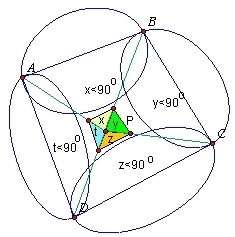
Ale w sumie te kąty powinny dać kąt pełny czyli o mierze 360 stopni. Coś tu nie gra ! Sami widzicie. Z tego wynika, że okręgi muszą pokryć cały czworokąt.