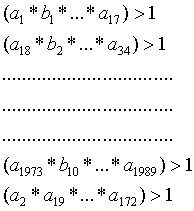LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA PRZYGOTOWAWCZE DO ETAPU IV
DLA GIMNAZJUM
ZADANIE 16
Danych jest 2000 liczb dodatnich. Uzasadnij, że jeśli iloczyn dowolnych siedemnastu z nich jest większy od 1, to iloczyn wszystkich tych liczb jest także większy od 1.
Rozwiązanie:
Na początku mamy taką sytuację:
Iloczyn wszystkich 2000 liczb możemy ująć w 117 ('pełnych') nawiasów po 17 liczb, których iloczyn jest większy od 1 i na końcu w nawias, w którym znajduje się 10 liczb. O tym nawiasie nie wiem czy iloczyn w nim zawarty jest większy od 1. Wiem natomiast, że w każdym z 'pełnych' nawiasów znajduje się cyfra większa od 1. Wiem to stąd, że gdyby takiej liczby nie było to iloczyn liczb mniejszych od 1 byłby mniejszy od 1, a z treści zadania wiem, że tak nie jest. Moje ustawienie tych liczb jest takie, że w każdym 'pełnym' nawiasie druga liczba jest wieksza od 1.
Teraz wymieniam liczby z ostatniego, niepełnego nawiasu na liczby większe od 1 z dowolnych (np. początkowych dziesięciu) 'pełnych' nawiasów.
Po wymienieniu liczb z ostatniego nawiasu (będę na nie mówić b) mamy taką sytuację:
czyli iloczyn wszystkich nawiasów jest teraz większy od 1. Zadanie zostało rozwiązane.
Autor rozwiązania:
Paweł Kukiełczyński
e-mail: unforgiver@kki.net.pl