LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA SZKÓŁ PODSTAWOWYCH
Zadanie 16
Treść zadania
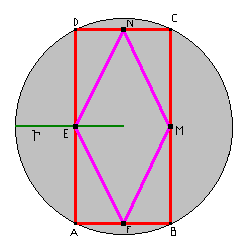
W okrąg o promieniu r wpisano prostokąt ABCD. Następnie połączono środki jego boków otrzymując czworokąt EFMN. Oblicz obwód otrzymanego prostokąta.
ROZWIĄZANIE
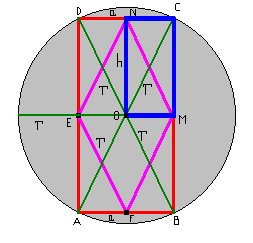
Prowadzimy promienie r tak, jak pokazuje to rysunek poniżej (promienie r zaznaczone są na zielono). Teraz tworzymy prostokąt NCMO (na rysunku narysowany jest na niebiesko). Jego przekątną jest promień r.
Korzystając z twierdzenia, które mówi, że przekątne w prostokącie są równe dochodzimy do tego, że odcinek NM równa się promieniowi r. Tworzymy inne takie prostokąty i dochodzimy do podobnego wniosku jak powyżej.
Wynika z tego, że otrzymany czworokąt (na rysunku narysowany na różowo) jest kwadratem.
Obwód jego więc wynosi 4r, co jest odpowiedzią na to zadanie.
Autor rozwiązania: Paweł Kukiełczyński
Kontakt:
*e-mail: Lord_Alkyd@poczta.wp.pl
telefon: 655-35-31